Data Amplification: Instance-Optimal Property Estimation
Paper and Code
Mar 05, 2019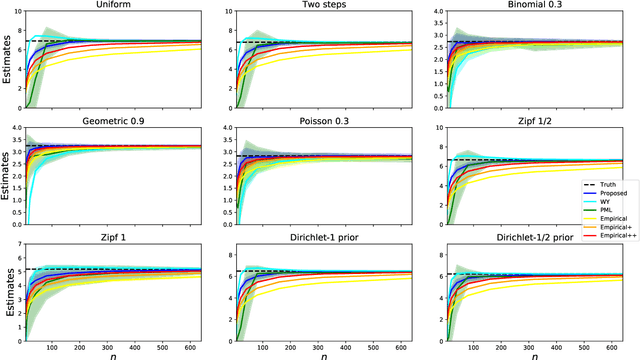
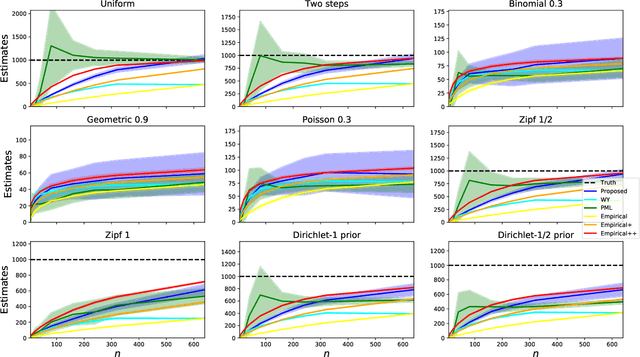
The best-known and most commonly used distribution-property estimation technique uses a plug-in estimator, with empirical frequency replacing the underlying distribution. We present novel linear-time-computable estimators that significantly "amplify" the effective amount of data available. For a large variety of distribution properties including four of the most popular ones and for every underlying distribution, they achieve the accuracy that the empirical-frequency plug-in estimators would attain using a logarithmic-factor more samples. Specifically, for Shannon entropy and a very broad class of properties including $\ell_1$-distance, the new estimators use $n$ samples to achieve the accuracy attained by the empirical estimators with $n\log n$ samples. For support-size and coverage, the new estimators use $n$ samples to achieve the performance of empirical frequency with sample size $n$ times the logarithm of the property value. Significantly strengthening the traditional min-max formulation, these results hold not only for the worst distributions, but for each and every underlying distribution. Furthermore, the logarithmic amplification factors are optimal. Experiments on a wide variety of distributions show that the new estimators outperform the previous state-of-the-art estimators designed for each specific property.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge