Data-Adaptive Probabilistic Likelihood Approximation for Ordinary Differential Equations

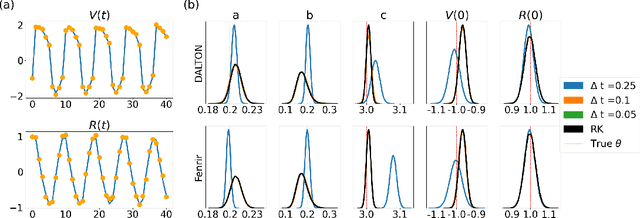
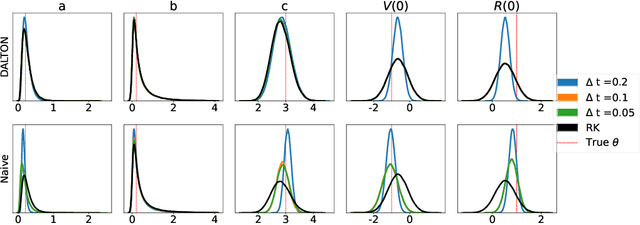
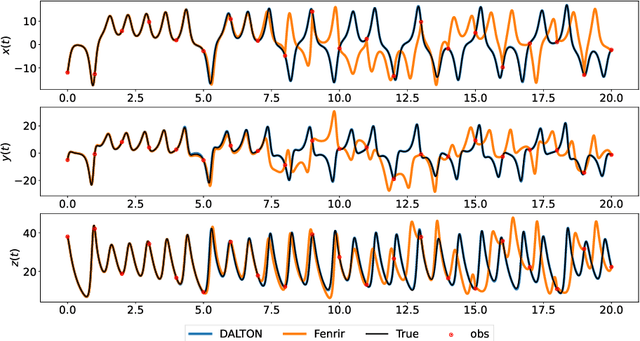
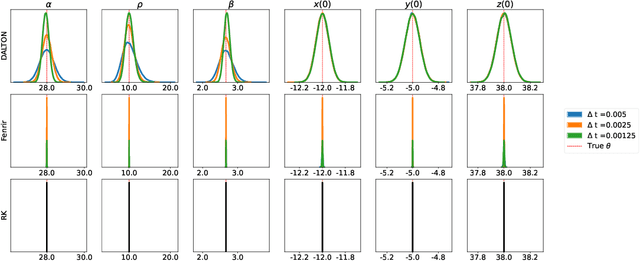
Parameter inference for ordinary differential equations (ODEs) is of fundamental importance in many scientific applications. While ODE solutions are typically approximated by deterministic algorithms, new research on probabilistic solvers indicates that they produce more reliable parameter estimates by better accounting for numerical errors. However, many ODE systems are highly sensitive to their parameter values. This produces deep local minima in the likelihood function -- a problem which existing probabilistic solvers have yet to resolve. Here, we show that a Bayesian filtering paradigm for probabilistic ODE solution can dramatically reduce sensitivity to parameters by learning from the noisy ODE observations in a data-adaptive manner. Our method is applicable to ODEs with partially unobserved components and with arbitrary non-Gaussian noise. Several examples demonstrate that it is more accurate than existing probabilistic ODE solvers, and even in some cases than the exact ODE likelihood.