DARC: Differentiable ARchitecture Compression
Paper and Code
May 20, 2019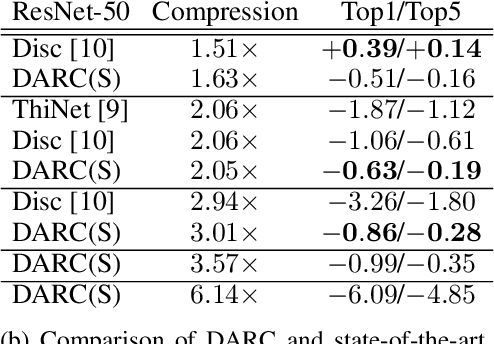
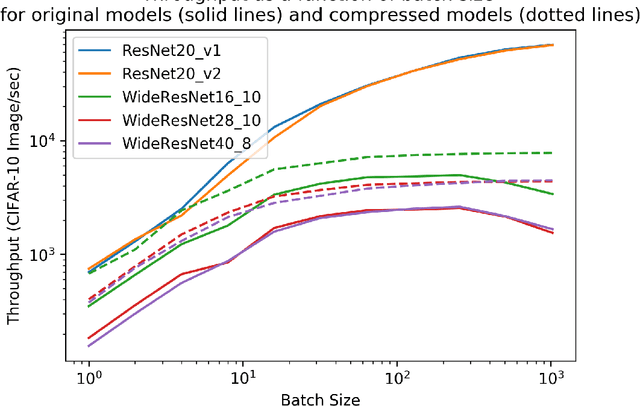
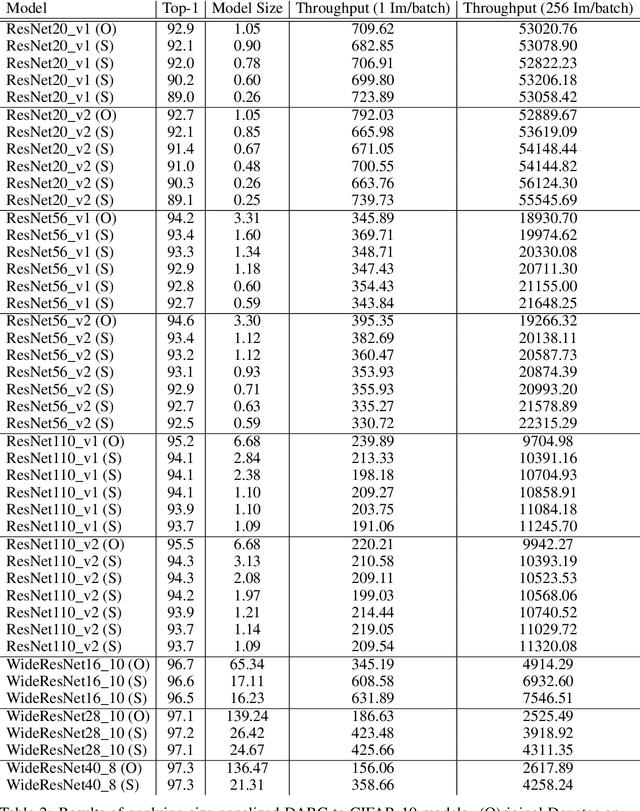
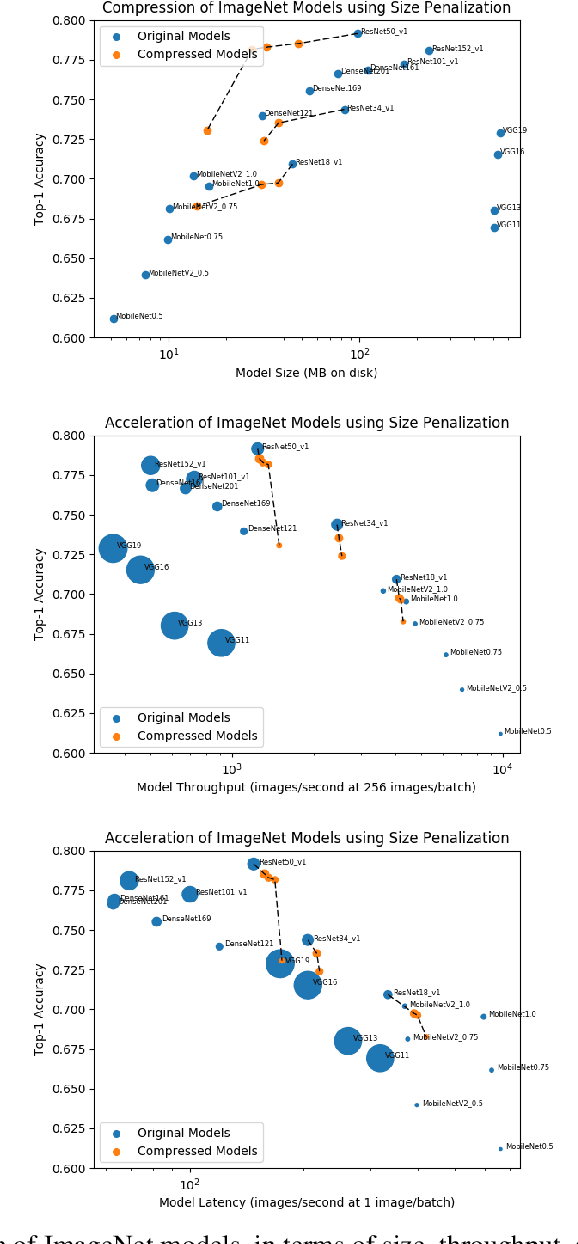
In many learning situations, resources at inference time are significantly more constrained than resources at training time. This paper studies a general paradigm, called Differentiable ARchitecture Compression (DARC), that combines model compression and architecture search to learn models that are resource-efficient at inference time. Given a resource-intensive base architecture, DARC utilizes the training data to learn which sub-components can be replaced by cheaper alternatives. The high-level technique can be applied to any neural architecture, and we report experiments on state-of-the-art convolutional neural networks for image classification. For a WideResNet with $97.2\%$ accuracy on CIFAR-10, we improve single-sample inference speed by $2.28\times$ and memory footprint by $5.64\times$, with no accuracy loss. For a ResNet with $79.15\%$ Top1 accuracy on ImageNet, we improve batch inference speed by $1.29\times$ and memory footprint by $3.57\times$ with $1\%$ accuracy loss. We also give theoretical Rademacher complexity bounds in simplified cases, showing how DARC avoids overfitting despite over-parameterization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge