DAG-WGAN: Causal Structure Learning With Wasserstein Generative Adversarial Networks
Paper and Code
Apr 01, 2022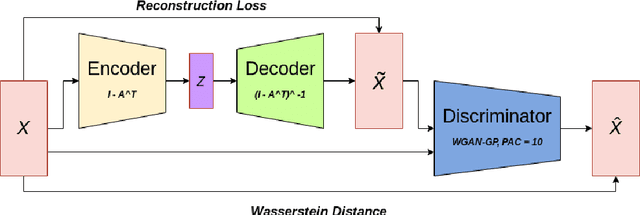
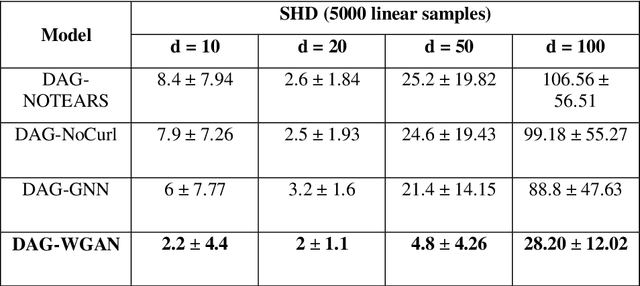
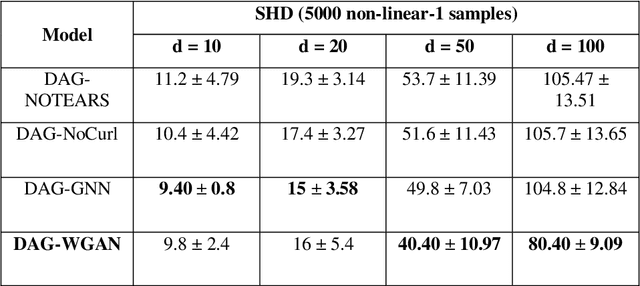
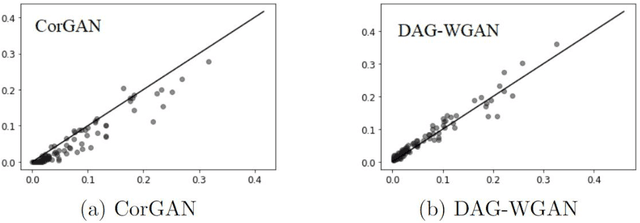
The combinatorial search space presents a significant challenge to learning causality from data. Recently, the problem has been formulated into a continuous optimization framework with an acyclicity constraint, allowing for the exploration of deep generative models to better capture data sample distributions and support the discovery of Directed Acyclic Graphs (DAGs) that faithfully represent the underlying data distribution. However, so far no study has investigated the use of Wasserstein distance for causal structure learning via generative models. This paper proposes a new model named DAG-WGAN, which combines the Wasserstein-based adversarial loss, an auto-encoder architecture together with an acyclicity constraint. DAG-WGAN simultaneously learns causal structures and improves its data generation capability by leveraging the strength from the Wasserstein distance metric. Compared with other models, it scales well and handles both continuous and discrete data. Our experiments have evaluated DAG-WGAN against the state-of-the-art and demonstrated its good performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge