D-SPIDER-SFO: A Decentralized Optimization Algorithm with Faster Convergence Rate for Nonconvex Problems
Paper and Code
Nov 28, 2019
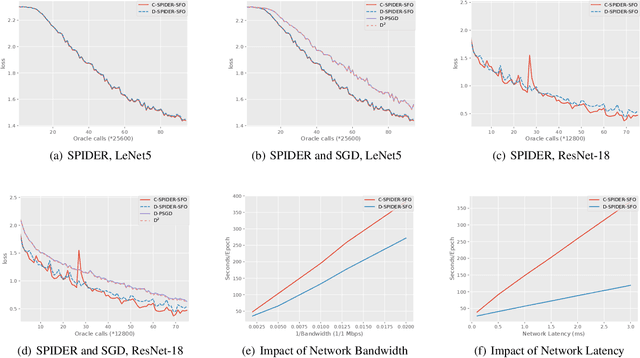
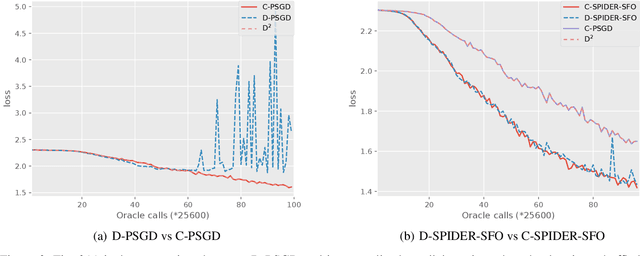
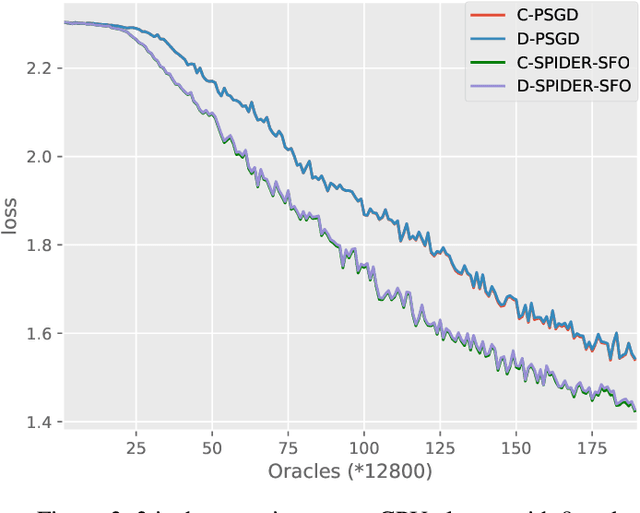
Decentralized optimization algorithms have attracted intensive interests recently, as it has a balanced communication pattern, especially when solving large-scale machine learning problems. Stochastic Path Integrated Differential Estimator Stochastic First-Order method (SPIDER-SFO) nearly achieves the algorithmic lower bound in certain regimes for nonconvex problems. However, whether we can find a decentralized algorithm which achieves a similar convergence rate to SPIDER-SFO is still unclear. To tackle this problem, we propose a decentralized variant of SPIDER-SFO, called decentralized SPIDER-SFO (D-SPIDER-SFO). We show that D-SPIDER-SFO achieves a similar gradient computation cost---that is, $\mathcal{O}(\epsilon^{-3})$ for finding an $\epsilon$-approximate first-order stationary point---to its centralized counterpart. To the best of our knowledge, D-SPIDER-SFO achieves the state-of-the-art performance for solving nonconvex optimization problems on decentralized networks in terms of the computational cost. Experiments on different network configurations demonstrate the efficiency of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge