Covariate Distribution Aware Meta-learning
Paper and Code
Jul 08, 2020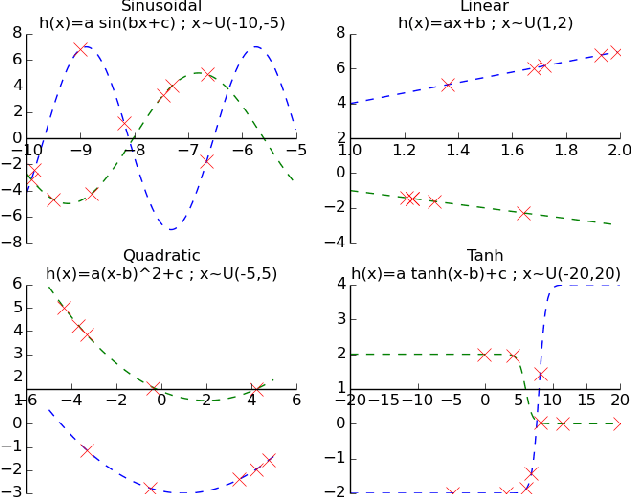
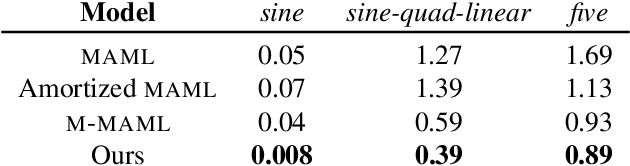
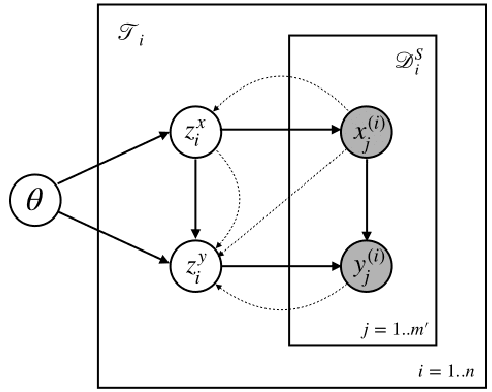
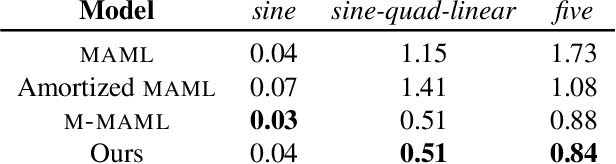
Meta-learning has proven to be successful at few-shot learning across the regression, classification and reinforcement learning paradigms. Recent approaches have adopted Bayesian interpretations to improve gradient based meta-learners by quantifying the uncertainty of the post-adaptation estimates. Most of these works almost completely ignore the latent relationship between the covariate distribution (p(x)) of a task and the corresponding conditional distribution p(y|x). In this paper, we identify the need to explicitly model the meta-distribution over the task covariates in a hierarchical Bayesian framework. We begin by introducing a graphical model that explicitly leverages very few samples drawn from p(x) to better infer the posterior over the optimal parameters of the conditional distribution (p(y|x)) for each task. Based on this model we provide an inference strategy and a corresponding meta-algorithm that explicitly accounts for the meta-distribution over task covariates. Finally, we demonstrate the significant gains of our proposed algorithm on a synthetic regression dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge