Correspondenceless scan-to-map-scan matching of homoriented 2D scans for mobile robot localisation

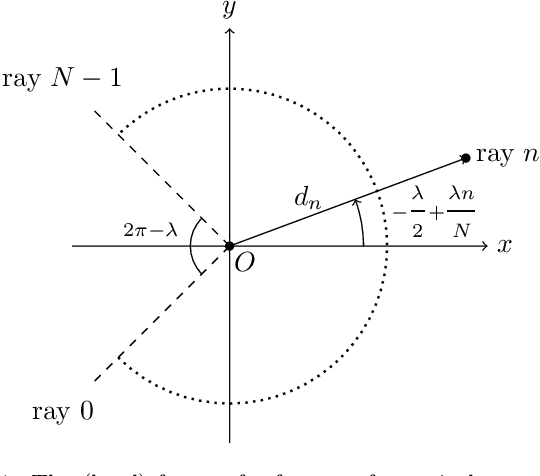
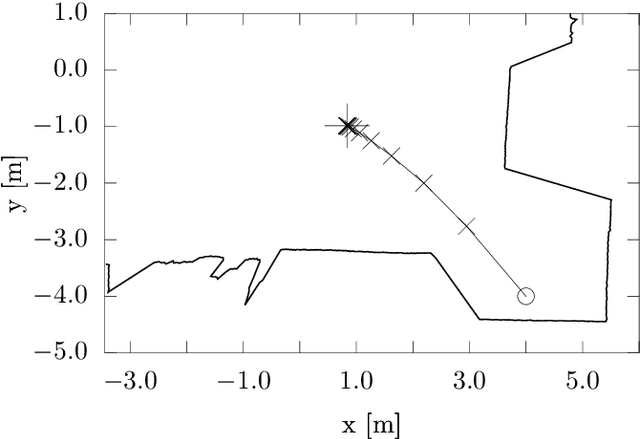
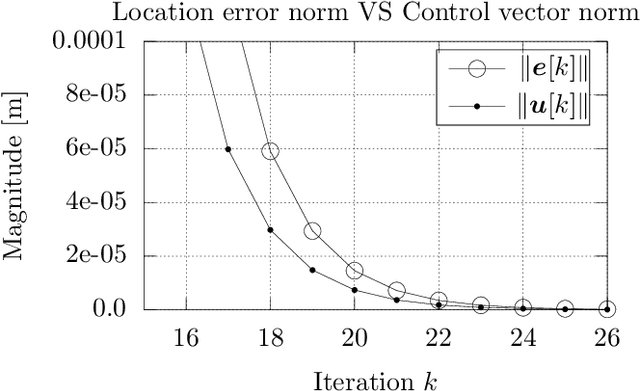
The objective of this study is improving the location estimate of a mobile robot capable of motion on a plane and mounted with a conventional 2D LIDAR sensor, given an initial guess for its location on a 2D map of its surroundings. Documented herein is the theoretical reasoning behind solving a matching problem between two homoriented 2D scans, one derived from the robot's physical sensor and one derived by simulating its operation within the map, in a manner that does not require the establishing of correspondences between their constituting rays. Two results are proved and subsequently shown through experiments. The first is that the true position of the sensor can be recovered with arbitrary precision when the physical sensor reports faultless measurements and there is no discrepancy between the environment the robot operates in and its perception of it by the robot. The second is that when either is affected by disturbance, the location estimate is bound in a neighbourhood of the true location whose radius is proportional to the affecting disturbance.