Convolutional Layers Are Not Translation Equivariant

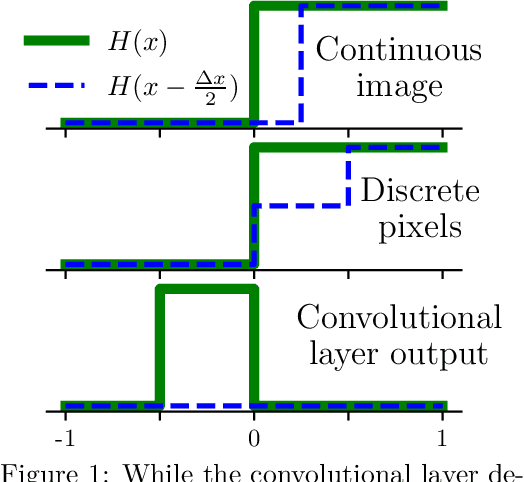
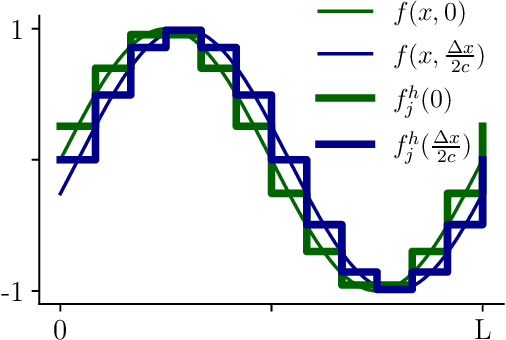
The purpose of this paper is to correct a misconception about convolutional neural networks (CNNs). CNNs are made up of convolutional layers which are shift equivariant due to weight sharing. However, contrary to popular belief, convolutional layers are not translation equivariant, even when boundary effects are ignored and when pooling and subsampling are absent. This is because shift equivariance is a discrete symmetry while translation equivariance is a continuous symmetry. That discrete systems do not in general inherit continuous equivariances is a fundamental limitation of equivariant deep learning. We discuss two implications of this fact. First, CNNs have achieved success in image processing despite not inheriting the translation equivariance of the physical systems they model. Second, using CNNs to solve partial differential equations (PDEs) will not result in translation equivariant solvers.