Convergent Differential Privacy Analysis for General Federated Learning: the f-DP Perspective
Paper and Code
Aug 28, 2024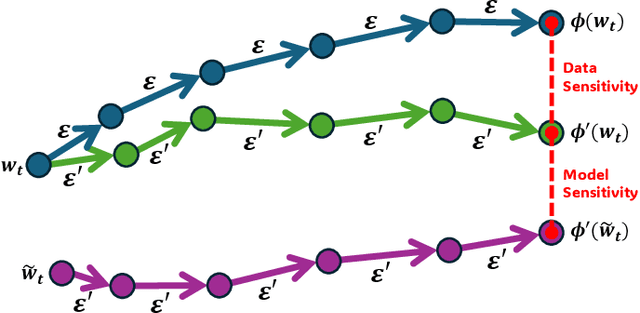
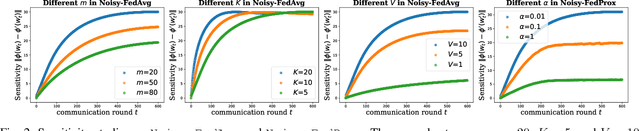
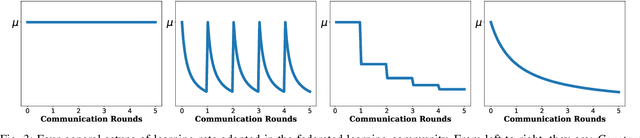

Federated learning (FL) is an efficient collaborative training paradigm extensively developed with a focus on local privacy protection, and differential privacy (DP) is a classical approach to capture and ensure the reliability of local privacy. The powerful cooperation of FL and DP provides a promising learning framework for large-scale private clients, juggling both privacy securing and trustworthy learning. As the predominant algorithm of DP, the noisy perturbation has been widely studied and incorporated into various federated algorithms, theoretically proven to offer significant privacy protections. However, existing analyses in noisy FL-DP mostly rely on the composition theorem and cannot tightly quantify the privacy leakage challenges, which is nearly tight for small numbers of communication rounds but yields an arbitrarily loose and divergent bound under the large communication rounds. This implies a counterintuitive judgment, suggesting that FL may not provide adequate privacy protection during long-term training. To further investigate the convergent privacy and reliability of the FL-DP framework, in this paper, we comprehensively evaluate the worst privacy of two classical methods under the non-convex and smooth objectives based on the f-DP analysis, i.e. Noisy-FedAvg and Noisy-FedProx methods. With the aid of the shifted-interpolation technique, we successfully prove that the worst privacy of the Noisy-FedAvg method achieves a tight convergent lower bound. Moreover, in the Noisy-FedProx method, with the regularization of the proxy term, the worst privacy has a stable constant lower bound. Our analysis further provides a solid theoretical foundation for the reliability of privacy protection in FL-DP. Meanwhile, our conclusions can also be losslessly converted to other classical DP analytical frameworks, e.g. $(\epsilon,\delta)$-DP and R$\acute{\text{e}}$nyi-DP (RDP).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge