Convergent Actor-Critic Algorithms Under Off-Policy Training and Function Approximation
Paper and Code
Feb 21, 2018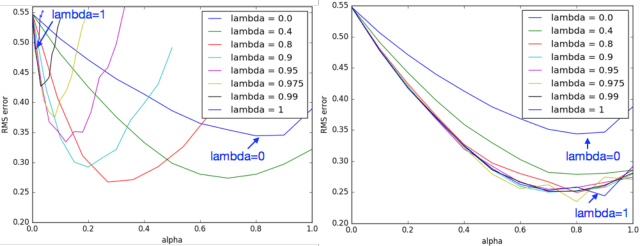
We present the first class of policy-gradient algorithms that work with both state-value and policy function-approximation, and are guaranteed to converge under off-policy training. Our solution targets problems in reinforcement learning where the action representation adds to the-curse-of-dimensionality; that is, with continuous or large action sets, thus making it infeasible to estimate state-action value functions (Q functions). Using state-value functions helps to lift the curse and as a result naturally turn our policy-gradient solution into classical Actor-Critic architecture whose Actor uses state-value function for the update. Our algorithms, Gradient Actor-Critic and Emphatic Actor-Critic, are derived based on the exact gradient of averaged state-value function objective and thus are guaranteed to converge to its optimal solution, while maintaining all the desirable properties of classical Actor-Critic methods with no additional hyper-parameters. To our knowledge, this is the first time that convergent off-policy learning methods have been extended to classical Actor-Critic methods with function approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge