Convergence of Krasulina Scheme
Paper and Code
Aug 28, 2018
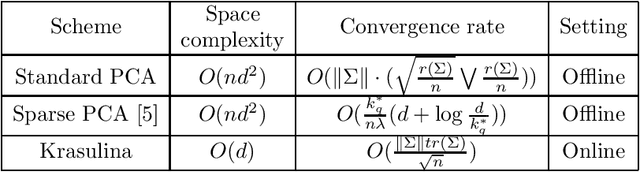
Principal component analysis (PCA) is one of the most commonly used statistical procedures with a wide range of applications. Consider the points $X_1, X_2,..., X_n$ are vectors drawn i.i.d. from a distribution with mean zero and covariance $\Sigma$, where $\Sigma$ is unknown. Let $A_n = X_nX_n^T$, then $E[A_n] = \Sigma$. This paper consider the problem of finding the least eigenvalue and eigenvector of matrix $\Sigma$. A classical such estimator are due to Krasulina\cite{krasulina_method_1969}. We are going to state the convergence proof of Krasulina for the least eigenvalue and corresponding eigenvector, and then find their convergence rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge