Convergence bounds for nonlinear least squares for tensor recovery

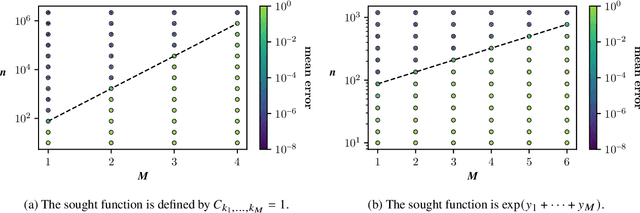
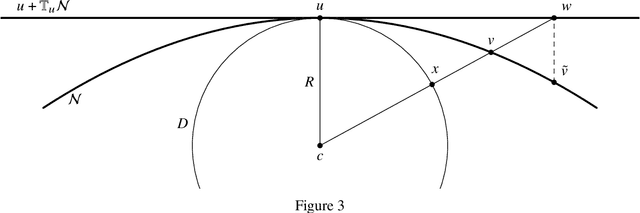
We consider the problem of approximating a function in general nonlinear subsets of L2 when only a weighted Monte Carlo estimate of the L2-norm can be computed. Of particular interest in this setting is the concept of sample complexity, the number of sample points that are necessary to achieve a prescribed error with high probability. Reasonable worst-case bounds for this quantity exist only for particular subsets of L2, like linear spaces or sets of sparse vectors. For more general subsets, like tensor networks, the currently existing bounds are very pessimistic. By restricting the model class to a neighbourhood of the best approximation, we can derive improved worst-case bounds for the sample complexity. When the considered neighbourhood is a manifold with positive local reach, the sample complexity can be estimated by the sample complexity of the tangent space and the product of the sample complexity of the normal space and the manifold's curvature.