Convergence and finite sample approximations of entropic regularized Wasserstein distances in Gaussian and RKHS settings
Paper and Code
Jan 05, 2021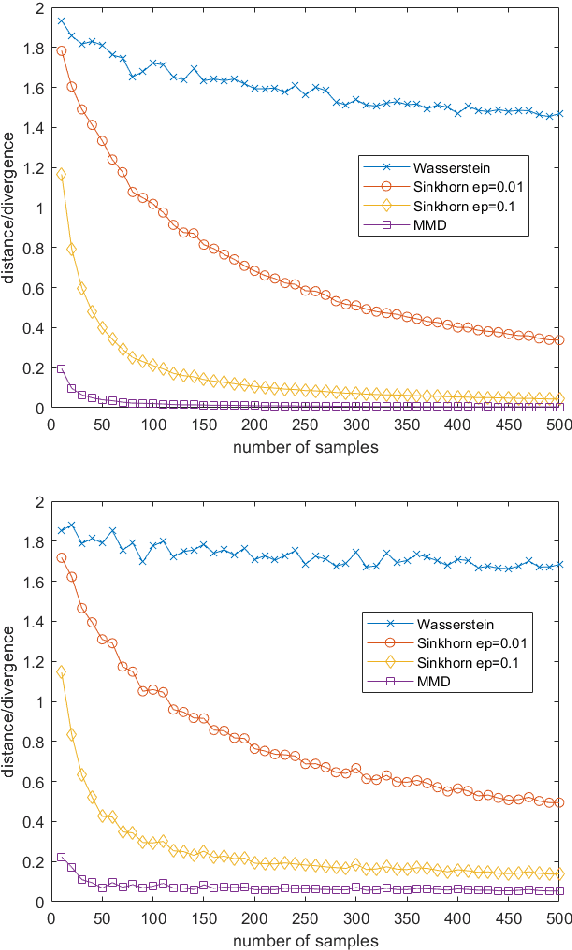
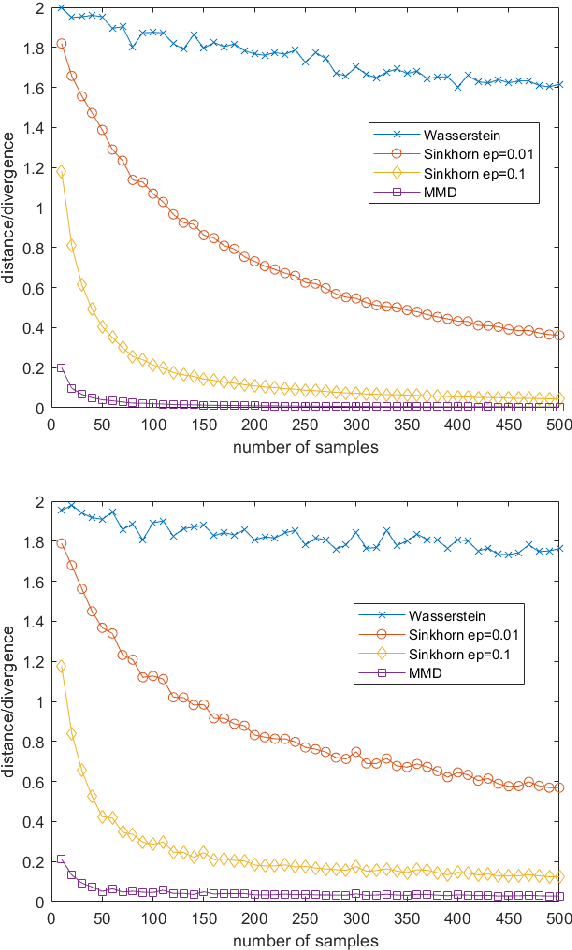
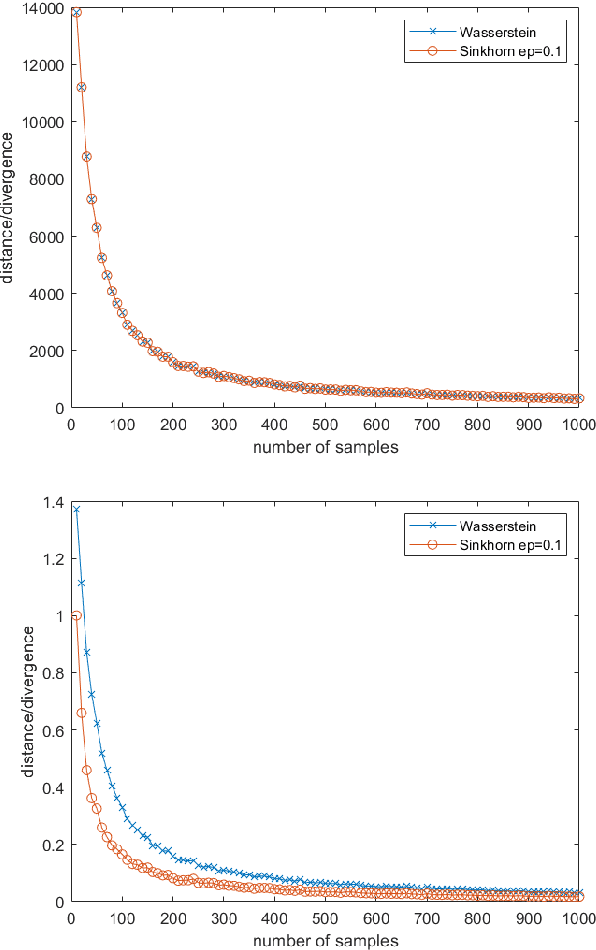
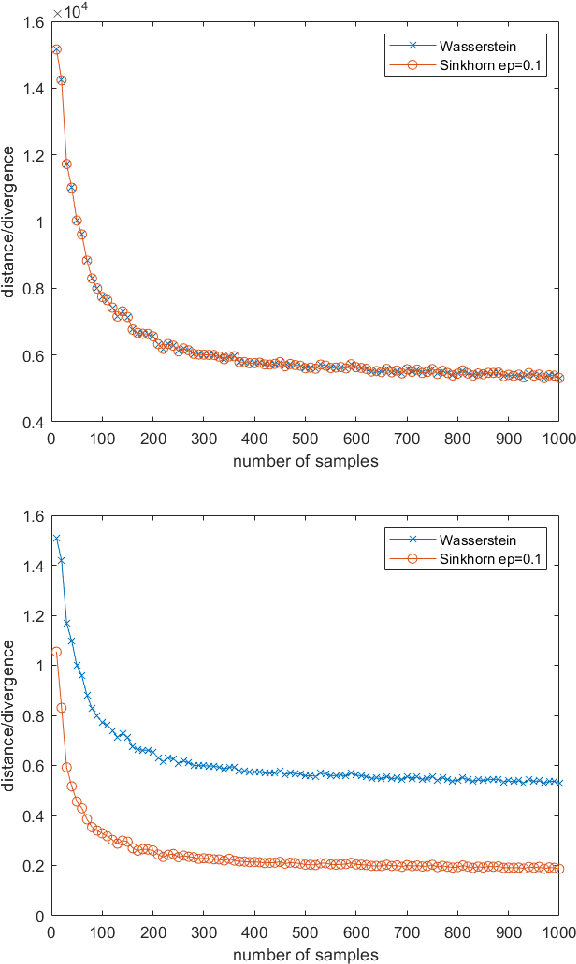
This work studies the convergence and finite sample approximations of entropic regularized Wasserstein distances in the Hilbert space setting. Our first main result is that for Gaussian measures on an infinite-dimensional Hilbert space, convergence in the 2-Sinkhorn divergence is {\it strictly weaker} than convergence in the exact 2-Wasserstein distance. Specifically, a sequence of centered Gaussian measures converges in the 2-Sinkhorn divergence if the corresponding covariance operators converge in the Hilbert-Schmidt norm. This is in contrast to the previous known result that a sequence of centered Gaussian measures converges in the exact 2-Wasserstein distance if and only if the covariance operators converge in the trace class norm. In the reproducing kernel Hilbert space (RKHS) setting, the {\it kernel Gaussian-Sinkhorn divergence}, which is the Sinkhorn divergence between Gaussian measures defined on an RKHS, defines a semi-metric on the set of Borel probability measures on a Polish space, given a characteristic kernel on that space. With the Hilbert-Schmidt norm convergence, we obtain {\it dimension-independent} convergence rates for finite sample approximations of the kernel Gaussian-Sinkhorn divergence, with the same order as the Maximum Mean Discrepancy. These convergence rates apply in particular to Sinkhorn divergence between Gaussian measures on Euclidean and infinite-dimensional Hilbert spaces. The sample complexity for the 2-Wasserstein distance between Gaussian measures on Euclidean space, while dimension-dependent and larger than that of the Sinkhorn divergence, is exponentially faster than the worst case scenario in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge