Continuous Encryption Functions for Security Over Networks
Paper and Code
Nov 04, 2021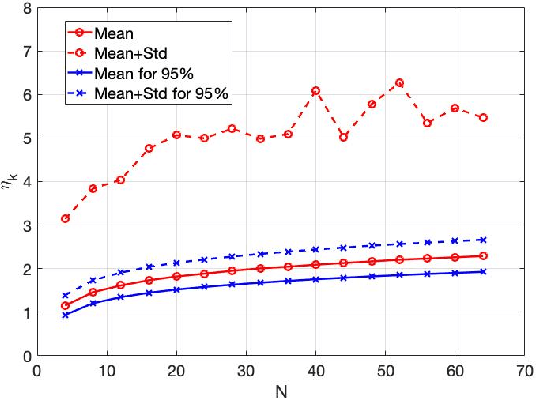
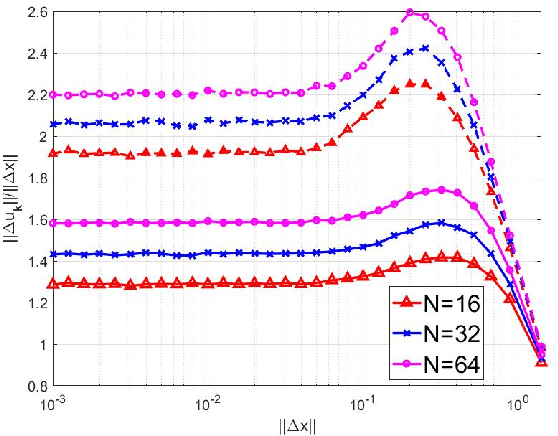
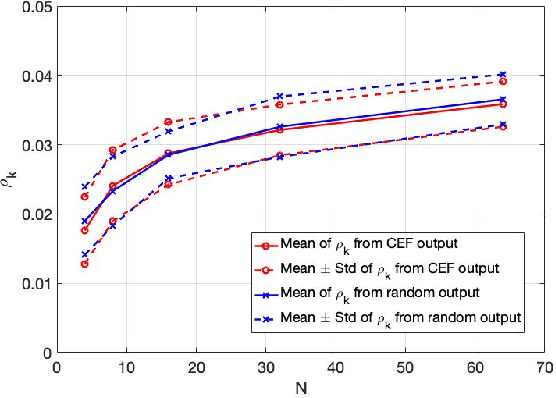
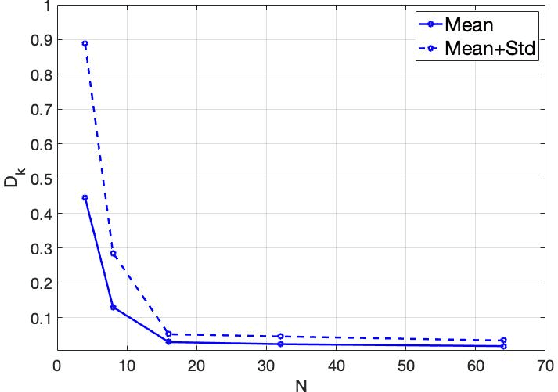
This paper presents a study of continuous encryption functions (CEFs) of secret feature vectors for security over networks such as physical layer encryption for wireless communications and biometric template security for online Internet applications. CEFs are defined to include all prior continuous "one-way" functions. It is shown that dynamic random projection and index-of-max (IoM) hashing algorithm 1 are not hard to attack, IoM algorithm 2 is not as hard to attack as it was thought to be, and higher-order polynomials are easy to attack via substitution. Also presented is a new family of CEFs based on selected components of singular value decomposition (SVD) of a randomly modulated matrix of feature vector. Detailed empirical evidence suggests that SVD-CEF is hard to attack. Statistical analysis of SVD-CEF reveals its useful properties including its sensitivity to noise. The bit-error-rate performance of a quantized SVD-CEF is shown to exceed that of IoM algorithm 2.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge