Continuous Dynamic-NeRF: Spline-NeRF
Paper and Code
Mar 25, 2022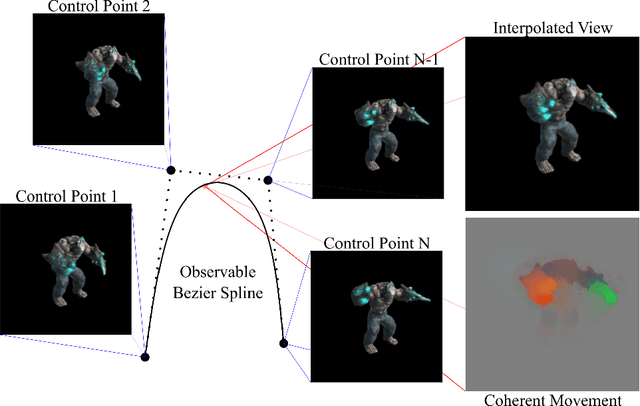
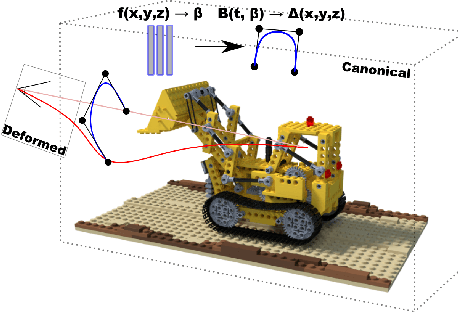
The problem of reconstructing continuous functions over time is important for problems such as reconstructing moving scenes, and interpolating between time steps. Previous approaches that use deep-learning rely on regularization to ensure that reconstructions are approximately continuous, which works well on short sequences. As sequence length grows, though, it becomes more difficult to regularize, and it becomes less feasible to learn only through regularization. We propose a new architecture for function reconstruction based on classical Bezier splines, which ensures $C^0$ and $C^1$-continuity, where $C^0$ continuity is that $\forall c:\lim\limits_{x\to c} f(x) = f(c)$, or more intuitively that there are no breaks at any point in the function. In order to demonstrate our architecture, we reconstruct dynamic scenes using Neural Radiance Fields, but hope it is clear that our approach is general and can be applied to a variety of problems. We recover a Bezier spline $B(\beta, t\in[0,1])$, parametrized by the control points $\beta$. Using Bezier splines ensures reconstructions have $C^0$ and $C^1$ continuity, allowing for guaranteed interpolation over time. We reconstruct $\beta$ with a multi-layer perceptron (MLP), blending machine learning with classical animation techniques. All code is available at https://github.com/JulianKnodt/nerf_atlas, and datasets are from prior work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge