Contextual Bandit Optimization with Pre-Trained Neural Networks

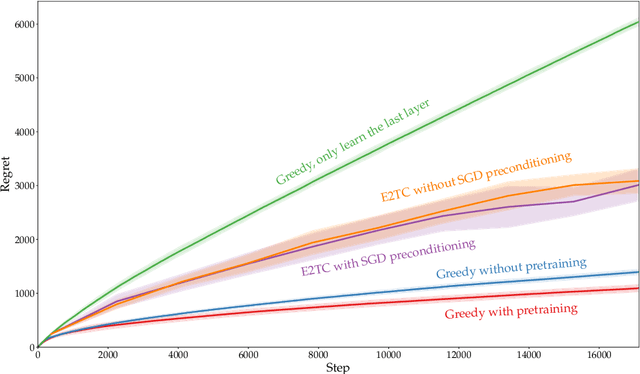
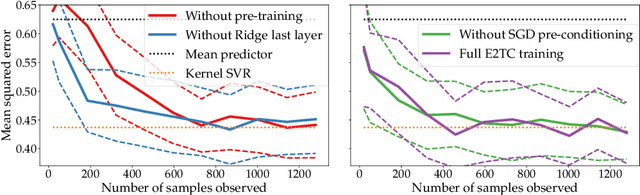
Bandit optimization is a difficult problem, especially if the reward model is high-dimensional. When rewards are modeled by neural networks, sublinear regret has only been shown under strong assumptions, usually when the network is extremely wide. In this thesis, we investigate how pre-training can help us in the regime of smaller models. We consider a stochastic contextual bandit with the rewards modeled by a multi-layer neural network. The last layer is a linear predictor, and the layers before it are a black box neural architecture, which we call a representation network. We model pre-training as an initial guess of the weights of the representation network provided to the learner. To leverage the pre-trained weights, we introduce a novel algorithm we call Explore Twice then Commit (E2TC). During its two stages of exploration, the algorithm first estimates the last layer's weights using Ridge regression, and then runs Stochastic Gradient Decent jointly on all the weights. For a locally convex loss function, we provide conditions on the pre-trained weights under which the algorithm can learn efficiently. Under these conditions, we show sublinear regret of E2TC when the dimension of the last layer and number of actions $K$ are much smaller than the horizon $T$. In the weak training regime, when only the last layer is learned, the problem reduces to a misspecified linear bandit. We introduce a measure of misspecification $\epsilon_0$ for this bandit and use it to provide bounds $O(\epsilon_0\sqrt{d}KT+(KT)^{4 /5})$ or $\tilde{O}(\epsilon_0\sqrt{d}KT+d^{1 /3}(KT)^{2 /3})$ on the regret, depending on regularization strength. The first of these bounds has a dimension-independent sublinear term, made possible by the stochasticity of contexts. We also run experiments to evaluate the regret of E2TC and sample complexity of its exploration in practice.