Constrained Optimization with Qualitative Preferences
Paper and Code
Sep 24, 2021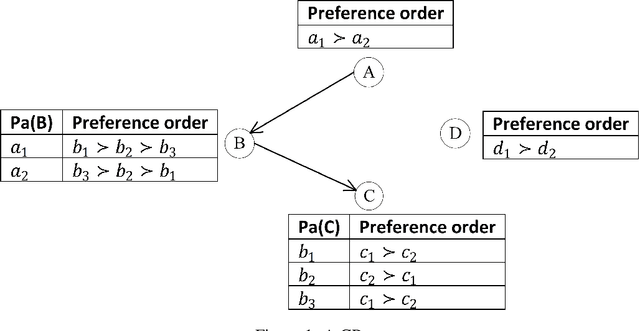
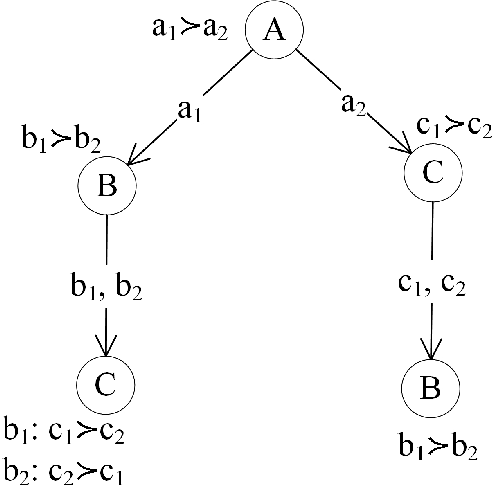
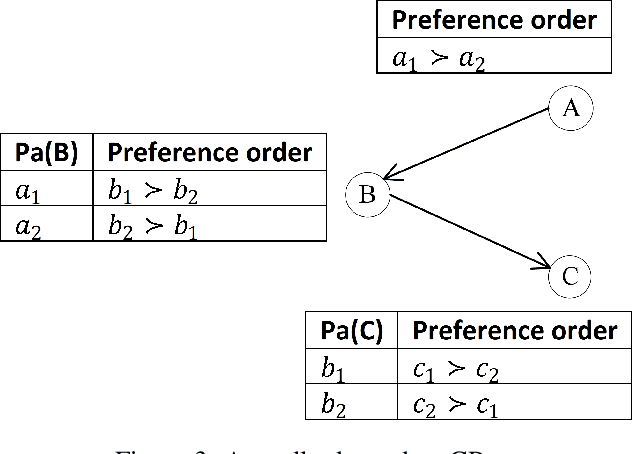
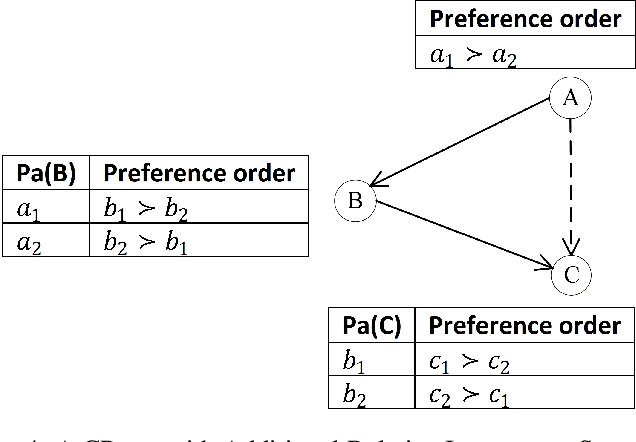
The Conditional Preference Network (CP-net) graphically represents user's qualitative and conditional preference statements under the ceteris paribus interpretation. The constrained CP-net is an extension of the CP-net, to a set of constraints. The existing algorithms for solving the constrained CP-net require the expensive dominance testing operation. We propose three approaches to tackle this challenge. In our first solution, we alter the constrained CP-net by eliciting additional relative importance statements between variables, in order to have a total order over the outcomes. We call this new model, the constrained Relative Importance Network (constrained CPR-net). Consequently, We show that the Constrained CPR-net has one single optimal outcome (assuming the constrained CPR-net is consistent) that we can obtain without dominance testing. In our second solution, we extend the Lexicographic Preference Tree (LP-tree) to a set of constraints. Then, we propose a recursive backtrack search algorithm, that we call Search-LP, to find the most preferable outcome. We prove that the first feasible outcome returned by Search-LP (without dominance testing) is also preferable to any other feasible outcome. Finally, in our third solution, we preserve the semantics of the CP-net and propose a divide and conquer algorithm that compares outcomes according to dominance testing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge