Conformal Predictions for Longitudinal Data
Paper and Code
Oct 04, 2023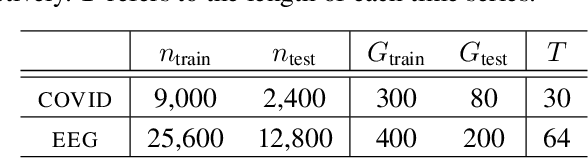
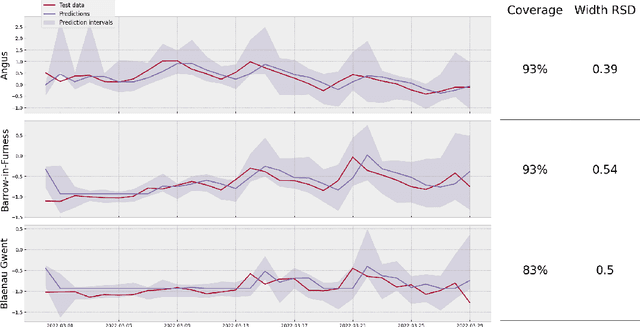

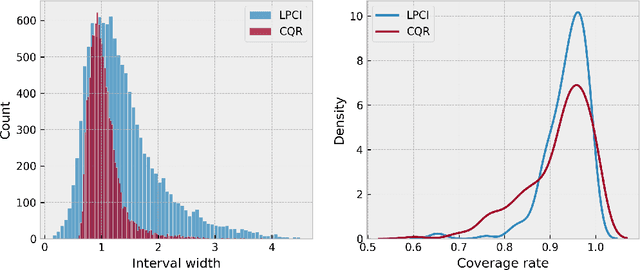
We introduce Longitudinal Predictive Conformal Inference (LPCI), a novel distribution-free conformal prediction algorithm for longitudinal data. Current conformal prediction approaches for time series data predominantly focus on the univariate setting, and thus lack cross-sectional coverage when applied individually to each time series in a longitudinal dataset. The current state-of-the-art for longitudinal data relies on creating infinitely-wide prediction intervals to guarantee both cross-sectional and asymptotic longitudinal coverage. The proposed LPCI method addresses this by ensuring that both longitudinal and cross-sectional coverages are guaranteed without resorting to infinitely wide intervals. In our approach, we model the residual data as a quantile fixed-effects regression problem, constructing prediction intervals with a trained quantile regressor. Our extensive experiments demonstrate that LPCI achieves valid cross-sectional coverage and outperforms existing benchmarks in terms of longitudinal coverage rates. Theoretically, we establish LPCI's asymptotic coverage guarantees for both dimensions, with finite-width intervals. The robust performance of LPCI in generating reliable prediction intervals for longitudinal data underscores its potential for broad applications, including in medicine, finance, and supply chain management.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge