Conflict-based Search for Multi-Robot Motion Planning with Kinodynamic Constraints
Paper and Code
Jul 01, 2022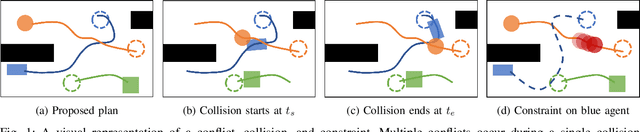


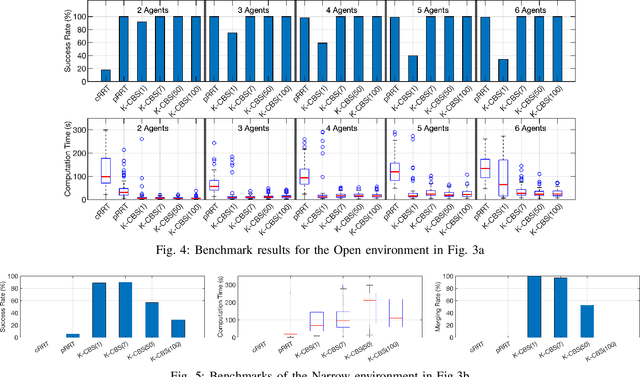
Multi-robot motion planning (MRMP) is the fundamental problem of finding non-colliding trajectories for multiple robots acting in an environment, under kinodynamic constraints. Due to its complexity, existing algorithms either utilize simplifying assumptions or are incomplete. This work introduces kinodynamic conflict-based search (K-CBS), a decentralized (decoupled) MRMP algorithm that is general, scalable, and probabilistically complete. The algorithm takes inspiration from successful solutions to the discrete analogue of MRMP over finite graphs, known as multi-agent path finding (MAPF). Specifically, we adapt ideas from conflict-based search (CBS) - a popular decentralized MAPF algorithm - to the MRMP setting. The novelty in this adaptation is that we work directly in the continuous domain, without the need for discretization. In particular, the kinodynamic constraints are treated natively. K-CBS plans for each robot individually using a low-level planner and and grows a conflict tree to resolve collisions between robots by defining constraints for individual robots. The low-level planner can be any sampling-based, tree-search algorithm for kinodynamic robots, thus lifting existing planners for single robots to the multi-robot settings. We show that K-CBS inherits the (probabilistic) completeness of the low-level planner. We illustrate the generality and performance of K-CBS in several case studies and benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge