Conditional probability calculation using restricted Boltzmann machine with application to system identification

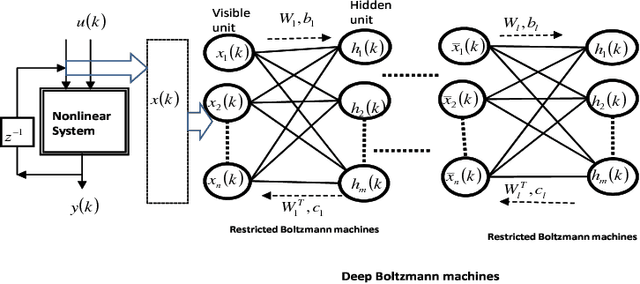
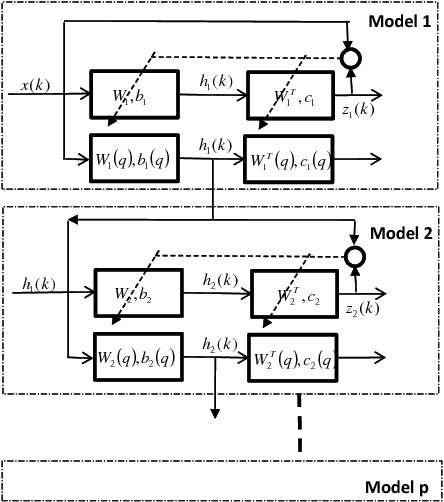
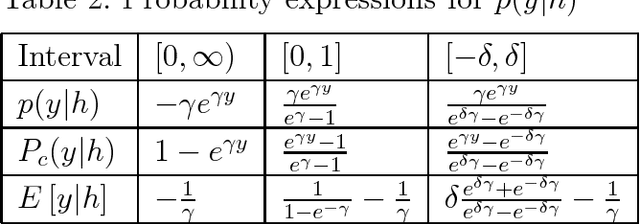
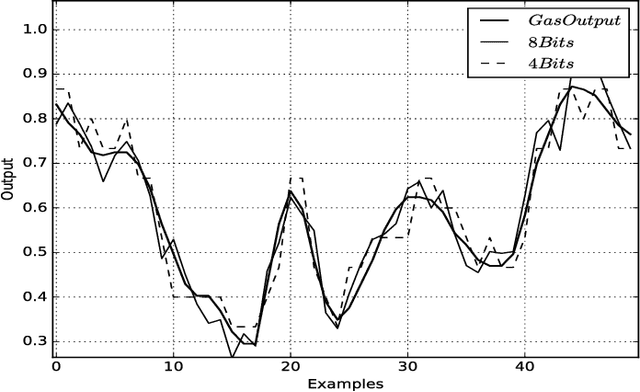
There are many advantages to use probability method for nonlinear system identification, such as the noises and outliers in the data set do not affect the probability models significantly; the input features can be extracted in probability forms. The biggest obstacle of the probability model is the probability distributions are not easy to be obtained. In this paper, we form the nonlinear system identification into solving the conditional probability. Then we modify the restricted Boltzmann machine (RBM), such that the joint probability, input distribution, and the conditional probability can be calculated by the RBM training. Binary encoding and continue valued methods are discussed. The universal approximation analysis for the conditional probability based modelling is proposed. We use two benchmark nonlinear systems to compare our probability modelling method with the other black-box modeling methods. The results show that this novel method is much better when there are big noises and the system dynamics are complex.