Computing CQ lower-bounds over OWL 2 through approximation to RSA
Paper and Code
Jul 01, 2021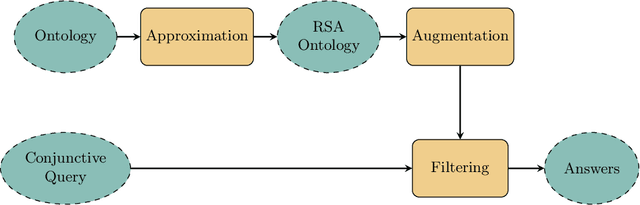

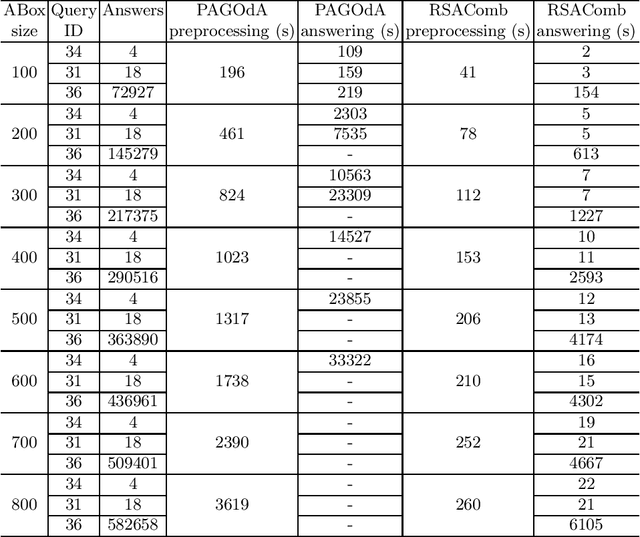

Conjunctive query (CQ) answering over knowledge bases is an important reasoning task. However, with expressive ontology languages such as OWL, query answering is computationally very expensive. The PAGOdA system addresses this issue by using a tractable reasoner to compute lower and upper-bound approximations, falling back to a fully-fledged OWL reasoner only when these bounds don't coincide. The effectiveness of this approach critically depends on the quality of the approximations, and in this paper we explore a technique for computing closer approximations via RSA, an ontology language that subsumes all the OWL 2 profiles while still maintaining tractability. We present a novel approximation of OWL 2 ontologies into RSA, and an algorithm to compute a closer (than PAGOdA) lower bound approximation using the RSA combined approach. We have implemented these algorithms in a prototypical CQ answering system, and we present a preliminary evaluation of our system that shows significant performance improvements w.r.t. PAGOdA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge