Computerized Tomography with Total Variation and with Shearlets
Paper and Code
Aug 23, 2016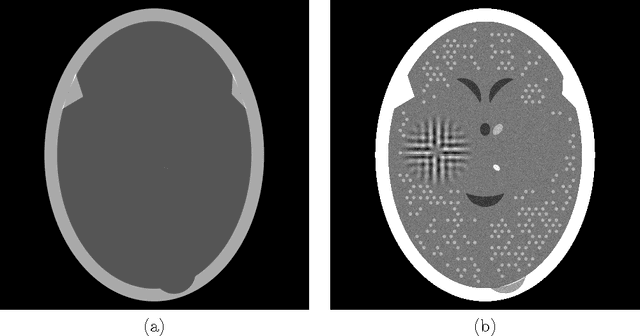
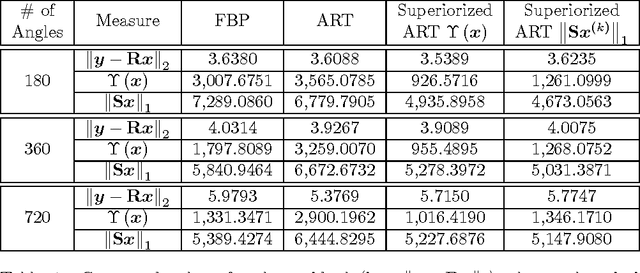
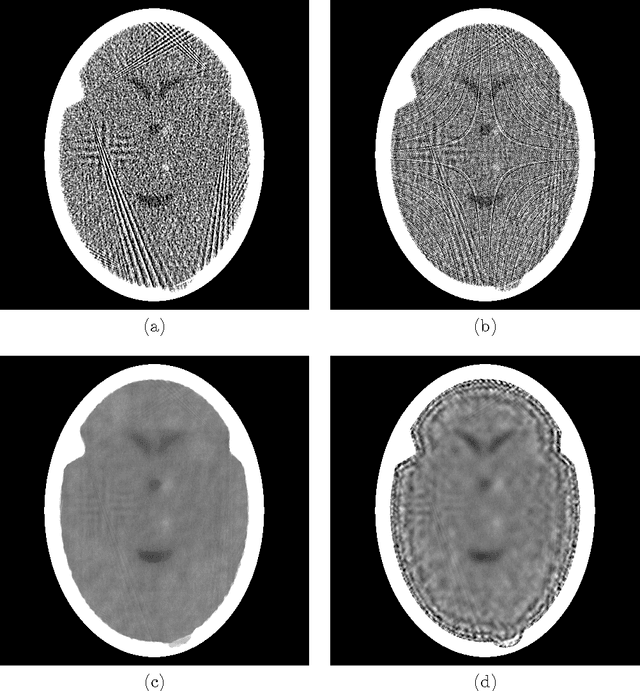
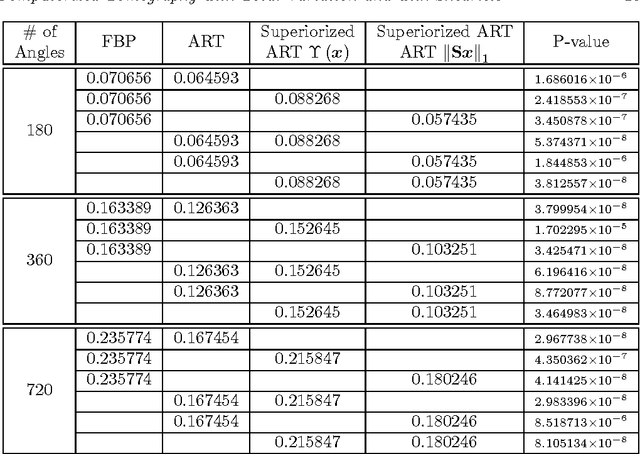
To reduce the x-ray dose in computerized tomography (CT), many constrained optimization approaches have been proposed aiming at minimizing a regularizing function that measures lack of consistency with some prior knowledge about the object that is being imaged, subject to a (predetermined) level of consistency with the detected attenuation of x-rays. Proponents of the shearlet transform in the regularizing function claim that the reconstructions so obtained are better than those produced using TV for texture preservation (but may be worse for noise reduction). In this paper we report results related to this claim. In our reported experiments using simulated CT data collection of the head, reconstructions whose shearlet transform has a small $\ell_1$-norm are not more efficacious than reconstructions that have a small TV value. Our experiments for making such comparisons use the recently-developed superiorization methodology for both regularizing functions. Superiorization is an automated procedure for turning an iterative algorithm for producing images that satisfy a primary criterion (such as consistency with the observed measurements) into its superiorized version that will produce results that, according to the primary criterion are as good as those produced by the original algorithm, but in addition are superior to them according to a secondary (regularizing) criterion. The method presented for superiorization involving the $\ell_1$-norm of the shearlet transform is novel and is quite general: It can be used for any regularizing function that is defined as the $\ell_1$-norm of a transform specified by the application of a matrix. Because in the previous literature the split Bregman algorithm is used for similar purposes, a section is included comparing the results of the superiorization algorithm with the split Bregman algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge