Computer-supported Analysis of Positive Properties, Ultrafilters and Modal Collapse in Variants of Gödel's Ontological Argument

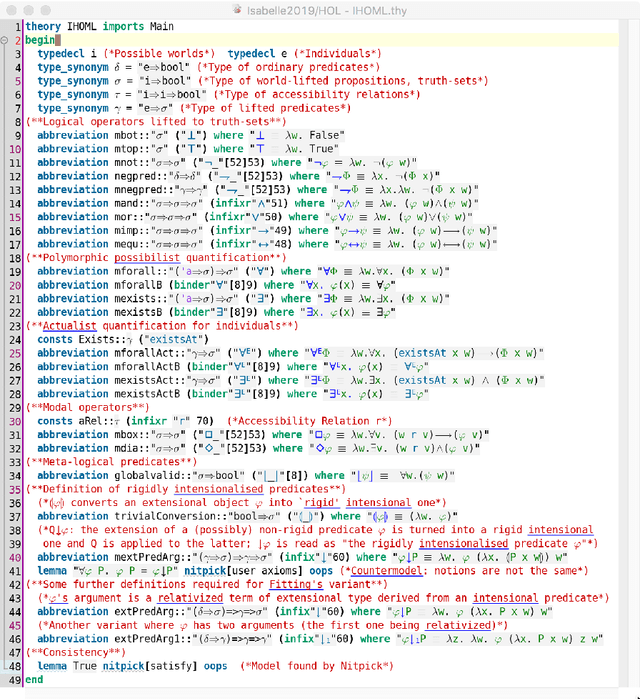
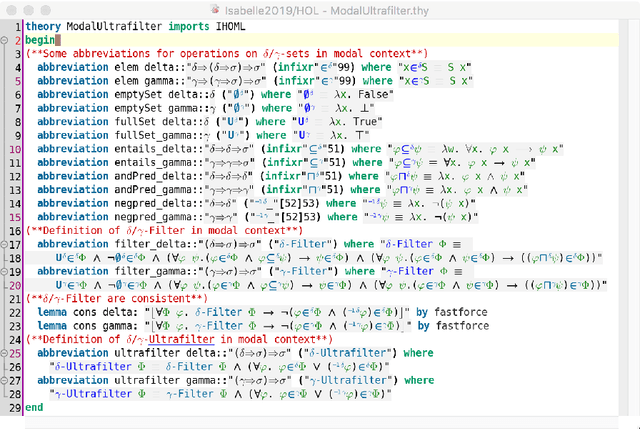
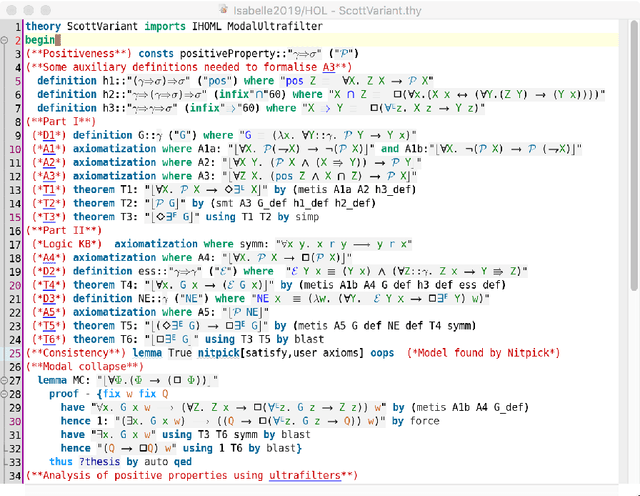
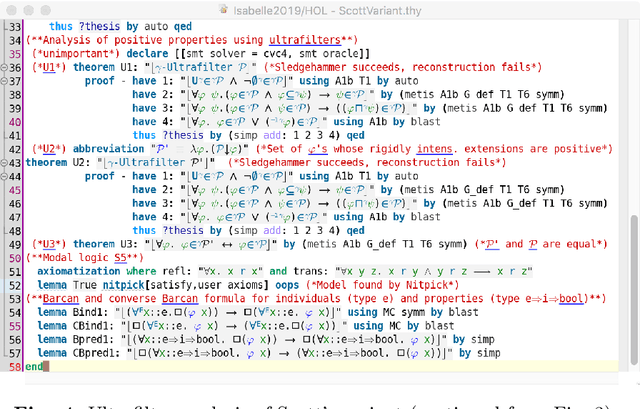
Three variants of Kurt G\"odel's ontological argument, as proposed byDana Scott, C. Anthony Anderson and Melvin Fitting, are encoded and rigorously assessed on the computer. In contrast to Scott's version of G\"odel's argument, the two variants contributed by Anderson and Fitting avoid modal collapse. Although they appear quite different on a cursory reading, they are in fact closely related, as our computer-supported formal analysis (conducted in the proof assistant system Isabelle/HOL) reveals. Key to our formal analysis is the utilization of suitably adapted notions of (modal) ultrafilters, and a careful distinction between extensions and intensions of positive properties.