Computationally-Optimal Real-Resource Strategies
Paper and Code
Mar 27, 2013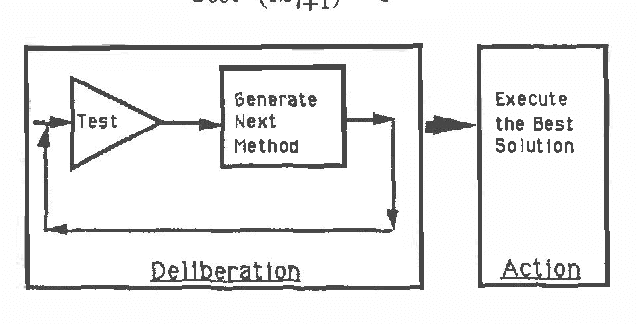
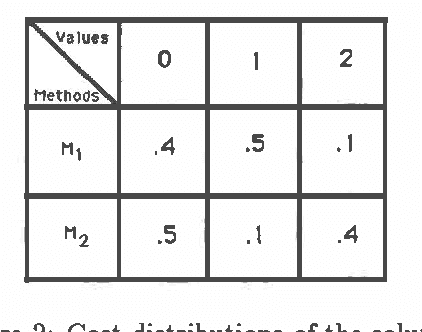
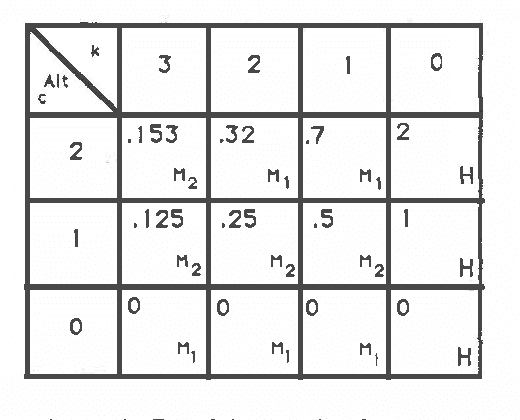
This paper focuses on managing the cost of deliberation before action. In many problems, the overall quality of the solution reflects costs incurred and resources consumed in deliberation as well as the cost and benefit of execution, when both the resource consumption in deliberation phase, and the costs in deliberation and execution are uncertain and may be described by probability distribution functions. A feasible (in terms of resource consumption) strategy that minimizes the expected total cost is termed computationally-optimal. For a situation with several independent, uninterruptible methods to solve the problem, we develop a pseudopolynomial-time algorithm to construct generate-and-test computationally optimal strategy. We show this strategy-construction problem to be NP-complete, and apply Bellman's Optimality Principle to solve it efficiently.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge