Computation of conditional expectations with guarantees
Paper and Code
Dec 03, 2021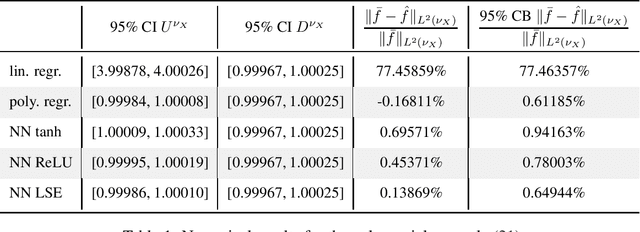
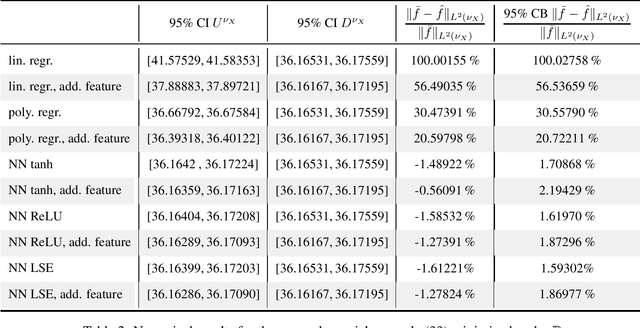
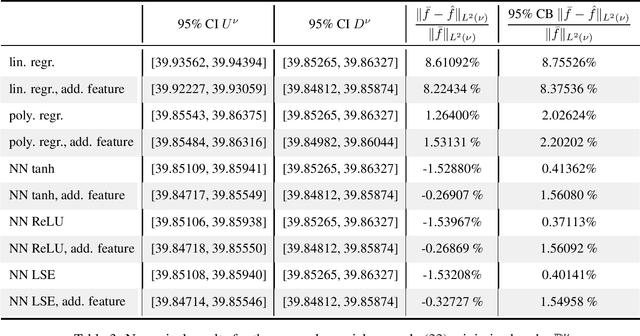
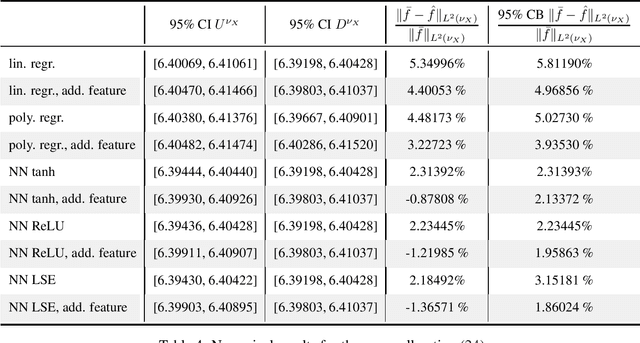
Theoretically, the conditional expectation of a square-integrable random variable $Y$ given a $d$-dimensional random vector $X$ can be obtained by minimizing the mean squared distance between $Y$ and $f(X)$ over all Borel measurable functions $f \colon \mathbb{R}^d \to \mathbb{R}$. However, in many applications this minimization problem cannot be solved exactly, and instead, a numerical method that computes an approximate minimum over a suitable subfamily of Borel functions has to be used. The quality of the result depends on the adequacy of the subfamily and the performance of the numerical method. In this paper, we derive an expected value representation of the minimal mean square distance which in many applications can efficiently be approximated with a standard Monte Carlo average. This enables us to provide guarantees for the accuracy of any numerical approximation of a given conditional expectation. We illustrate the method by assessing the quality of approximate conditional expectations obtained by linear, polynomial as well as neural network regression in different concrete examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge