Compressive Imaging using Approximate Message Passing and a Markov-Tree Prior
Paper and Code
Aug 12, 2011
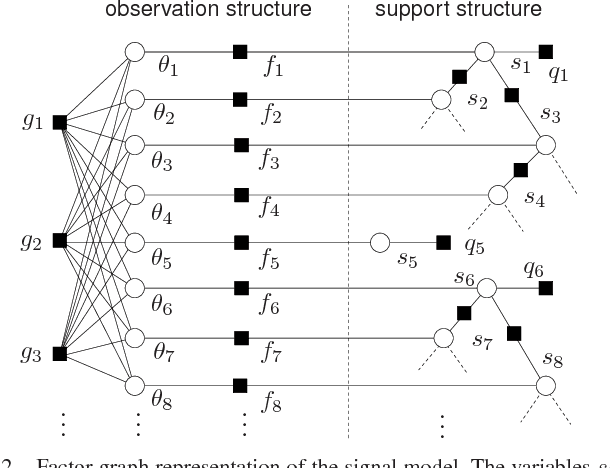
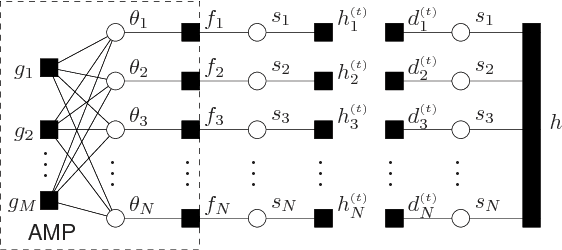

We propose a novel algorithm for compressive imaging that exploits both the sparsity and persistence across scales found in the 2D wavelet transform coefficients of natural images. Like other recent works, we model wavelet structure using a hidden Markov tree (HMT) but, unlike other works, ours is based on loopy belief propagation (LBP). For LBP, we adopt a recently proposed "turbo" message passing schedule that alternates between exploitation of HMT structure and exploitation of compressive-measurement structure. For the latter, we leverage Donoho, Maleki, and Montanari's recently proposed approximate message passing (AMP) algorithm. Experiments with a large image database suggest that, relative to existing schemes, our turbo LBP approach yields state-of-the-art reconstruction performance with substantial reduction in complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge