Comparing different subgradient methods for solving convex optimization problems with functional constraints
Paper and Code
Jan 04, 2021
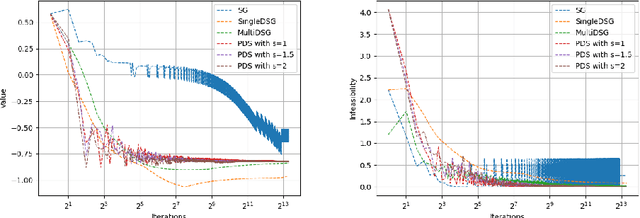

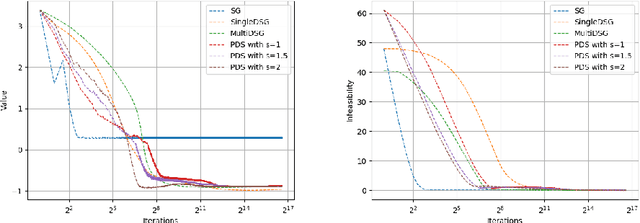
We provide a dual subgradient method and a primal-dual subgradient method for standard convex optimization problems with complexity $\mathcal{O}(\varepsilon^{-2})$ and $\mathcal{O}(\varepsilon^{-2r})$, for all $r> 1$, respectively. They are based on recent Metel-Takeda's work in [arXiv:2009.12769, 2020, pp. 1-12] and Boyd's method in [Lecture notes of EE364b, Stanford University, Spring 2013-14, pp. 1-39]. The efficiency of our methods is numerically illustrated in a comparison to the others.
* 25 pages, 10 tables, 15 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge