Communications under Bursty Mixed Gaussian-impulsive Noise: Demodulation and Performance Analysis
Paper and Code
May 09, 2024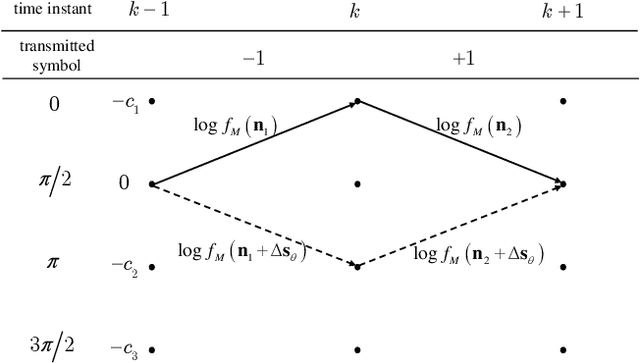
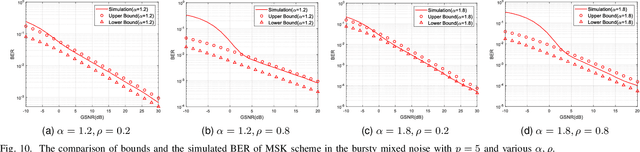
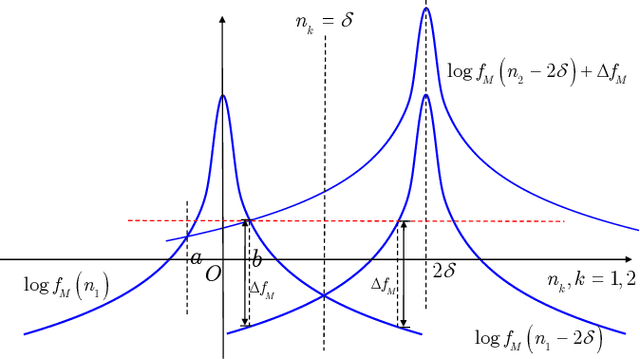
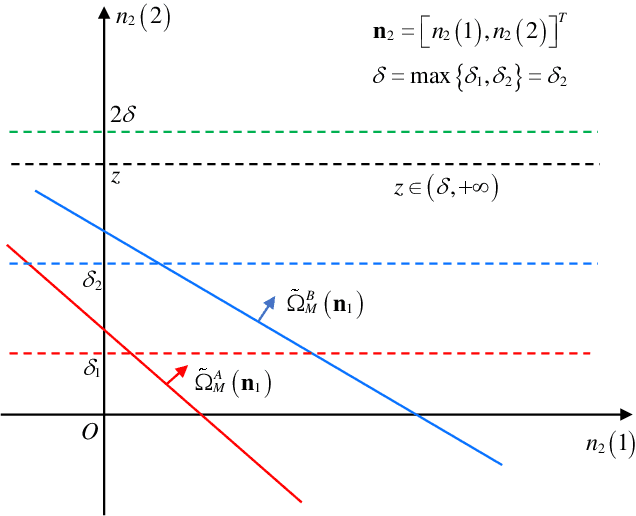
This is the second part of the two-part paper considering the communications under the bursty mixed noise composed of white Gaussian noise and colored non-Gaussian impulsive noise. In the first part, based on Gaussian distribution and student distribution, we proposed a multivariate bursty mixed noise model and designed model parameter estimation algorithms. However, the performance of a communication system will significantly deteriorate under the bursty mixed noise if a conventional signal detection algorithm with respect to Gaussian noise is applied. To address this issue, in the second part, we leverage the probability density function (PDF) to derive the maximum likelihood (ML) demodulation methods for both linear and nonlinear modulations, including M-array PSK (M-PSK) and MSK modulation schemes. We analyze the theoretical bit error rate (BER) performance of M-PSK and present close-form BER expressions. For the MSK demodulation based on the Viterbi algorithm, we derive a lower and upper bound of BER. Simulation results showcase that the proposed demodulation methods outperform baselines by more than 2.5dB when the BER performance reaches the order of magnitude of $10^{-3}$, and the theoretical analysis matches the simulated results well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge