Combining Natural Gradient with Hessian Free Methods for Sequence Training
Paper and Code
Oct 03, 2018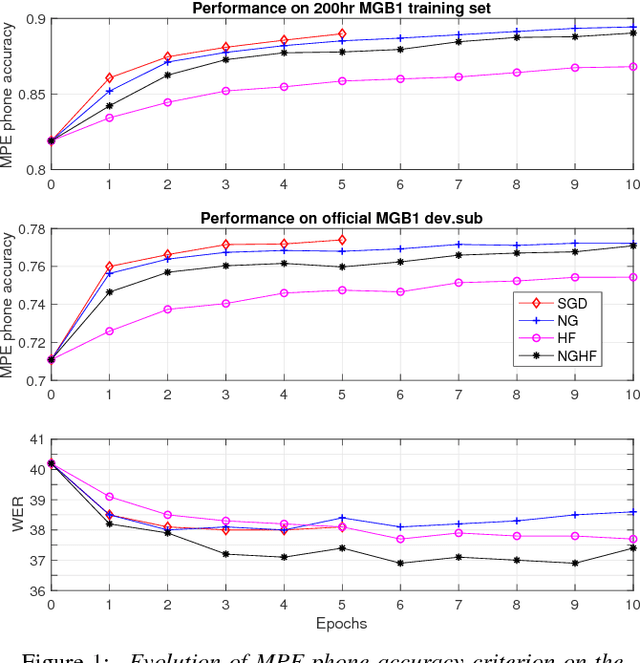
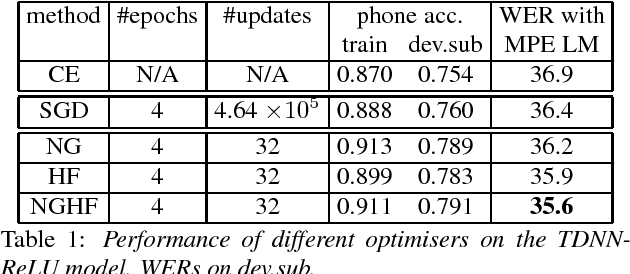
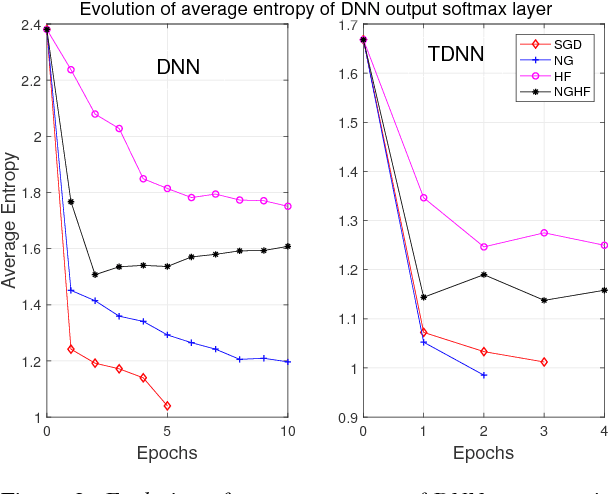
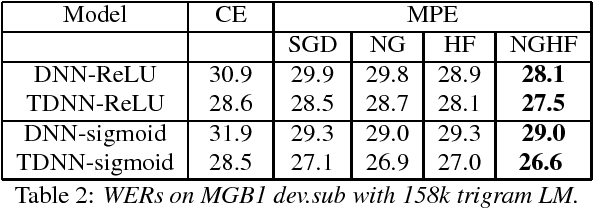
This paper presents a new optimisation approach to train Deep Neural Networks (DNNs) with discriminative sequence criteria. At each iteration, the method combines information from the Natural Gradient (NG) direction with local curvature information of the error surface that enables better paths on the parameter manifold to be traversed. The method is derived using an alternative derivation of Taylor's theorem using the concepts of manifolds, tangent vectors and directional derivatives from the perspective of Information Geometry. The efficacy of the method is shown within a Hessian Free (HF) style optimisation framework to sequence train both standard fully-connected DNNs and Time Delay Neural Networks as speech recognition acoustic models. It is shown that for the same number of updates the proposed approach achieves larger reductions in the word error rate (WER) than both NG and HF, and also leads to a lower WER than standard stochastic gradient descent. The paper also addresses the issue of over-fitting due to mismatch between training criterion and Word Error Rate (WER) that primarily arises during sequence training of ReLU-DNN models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge