Colour Terms: a Categorisation Model Inspired by Visual Cortex Neurons
Paper and Code
Sep 19, 2017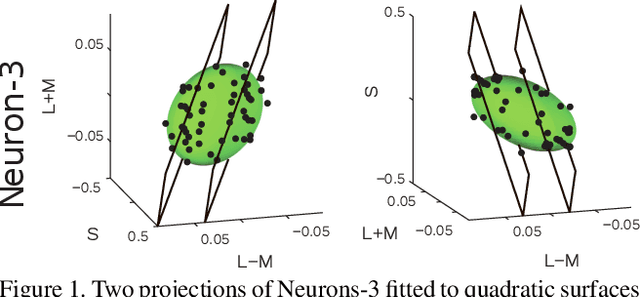
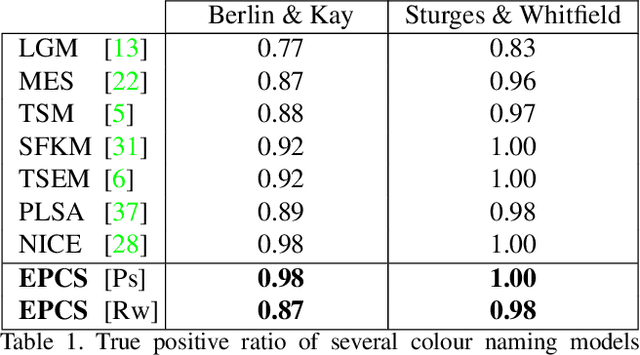
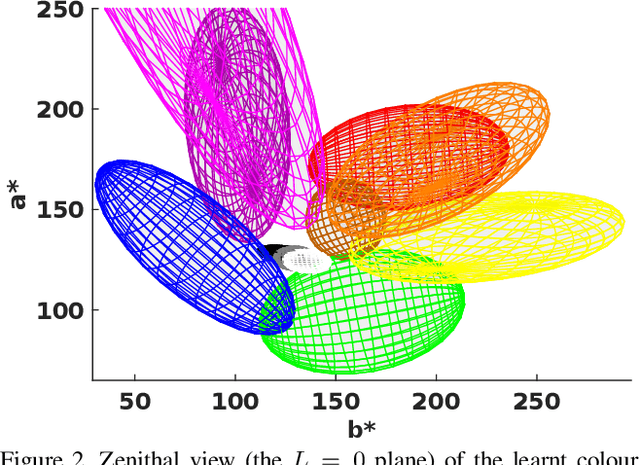
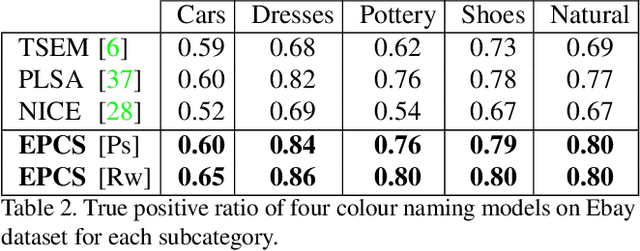
Although it seems counter-intuitive, categorical colours do not exist as external physical entities but are very much the product of our brains. Our cortical machinery segments the world and associate objects to specific colour terms, which is not only convenient for communication but also increases the efficiency of visual processing by reducing the dimensionality of input scenes. Although the neural substrate for this phenomenon is unknown, a recent study of cortical colour processing has discovered a set of neurons that are isoresponsive to stimuli in the shape of 3D-ellipsoidal surfaces in colour-opponent space. We hypothesise that these neurons might help explain the underlying mechanisms of colour naming in the visual cortex. Following this, we propose a biologically-inspired colour naming model where each colour term - e.g. red, green, blue, yellow, etc. - is represented through an ellipsoid in 3D colour-opponent space. This paradigm is also supported by previous psychophysical colour categorisation experiments whose results resemble such shapes. "Belongingness" of each pixel to different colour categories is computed by a non-linear sigmoidal logistic function. The final colour term for a given pixel is calculated by a maximum pooling mechanism. The simplicity of our model allows its parameters to be learnt from a handful of segmented images. It also offers a straightforward extension to include further colour terms. Additionally, ellipsoids of proposed model can adapt to image contents offering a dynamical solution in order to address phenomenon of colour constancy. Our results on the Munsell chart and two datasets of real-world images show an overall improvement comparing to state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge