Coherent structure coloring: identification of coherent structures from sparse data using graph theory
Paper and Code
Nov 07, 2016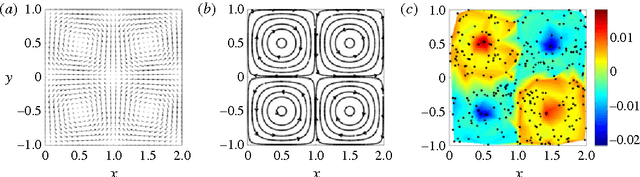

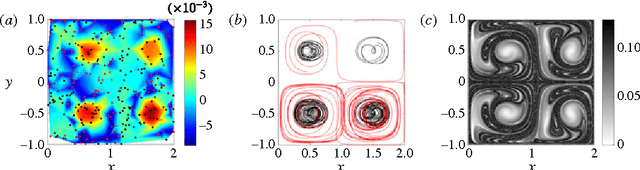
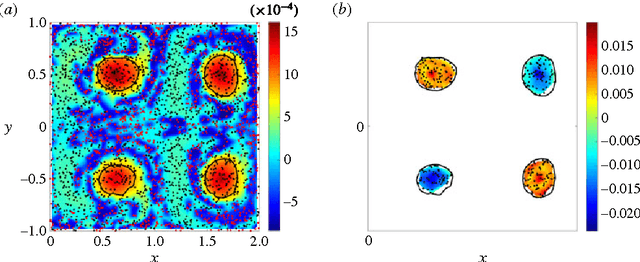
We present a frame-invariant method for detecting coherent structures from Lagrangian flow trajectories that can be sparse in number, as is the case in many fluid mechanics applications of practical interest. The method, based on principles used in graph coloring and spectral graph drawing algorithms, examines a measure of the kinematic dissimilarity of all pairs of fluid trajectories, either measured experimentally, e.g. using particle tracking velocimetry; or numerically, by advecting fluid particles in the Eulerian velocity field. Coherence is assigned to groups of particles whose kinematics remain similar throughout the time interval for which trajectory data is available, regardless of their physical proximity to one another. Through the use of several analytical and experimental validation cases, this algorithm is shown to robustly detect coherent structures using significantly less flow data than is required by existing spectral graph theory methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge