Coherent and Archimedean choice in general Banach spaces
Paper and Code
Feb 13, 2020
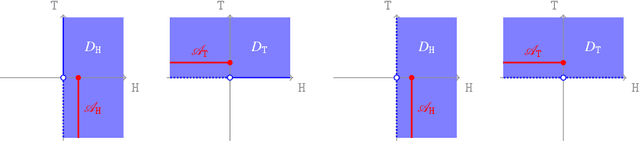
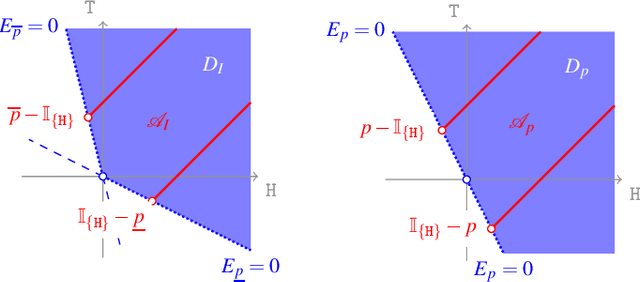
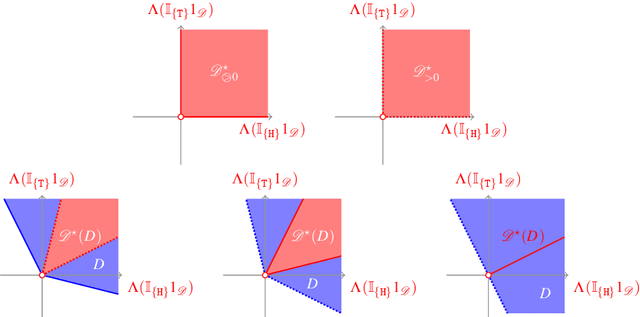
I introduce and study a new notion of Archimedeanity for binary and non-binary choice between options that live in an abstract Banach space, through a very general class of choice models, called sets of desirable option sets. In order to be able to bring horse lottery options into the fold, I pay special attention to the case where these linear spaces do not include all `constant' options. I consider the frameworks of conservative inference associated with Archimedean (and coherent) choice models, and also pay quite a lot of attention to representation of general (non-binary) choice models in terms of the simpler, binary ones. The representation theorems proved here provide an axiomatic characterisation of, amongst other choice methods, Levi's E-admissibility and Walley--Sen maximality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge