CMA-ES with Learning Rate Adaptation
Paper and Code
Jan 29, 2024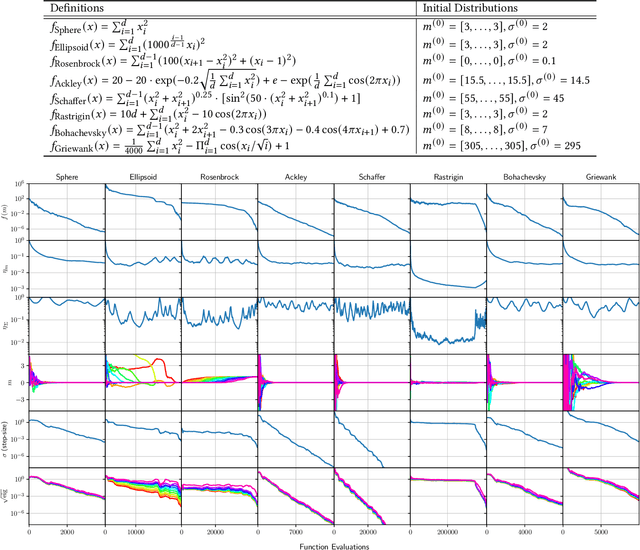

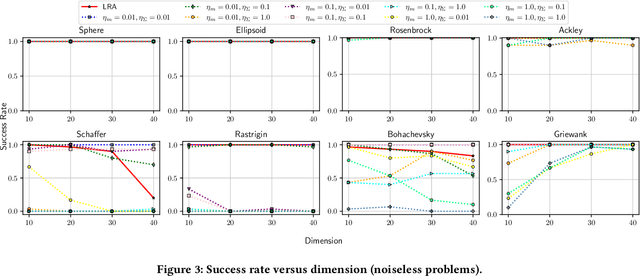
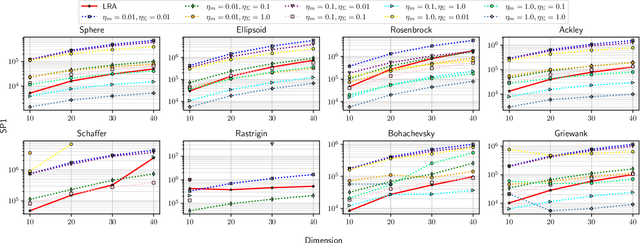
The covariance matrix adaptation evolution strategy (CMA-ES) is one of the most successful methods for solving continuous black-box optimization problems. A practically useful aspect of the CMA-ES is that it can be used without hyperparameter tuning. However, the hyperparameter settings still have a considerable impact on performance, especially for difficult tasks, such as solving multimodal or noisy problems. This study comprehensively explores the impact of learning rate on the CMA-ES performance and demonstrates the necessity of a small learning rate by considering ordinary differential equations. Thereafter, it discusses the setting of an ideal learning rate. Based on these discussions, we develop a novel learning rate adaptation mechanism for the CMA-ES that maintains a constant signal-to-noise ratio. Additionally, we investigate the behavior of the CMA-ES with the proposed learning rate adaptation mechanism through numerical experiments, and compare the results with those obtained for the CMA-ES with a fixed learning rate and with population size adaptation. The results show that the CMA-ES with the proposed learning rate adaptation works well for multimodal and/or noisy problems without extremely expensive learning rate tuning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge