Clustering with UMAP: Why and How Connectivity Matters

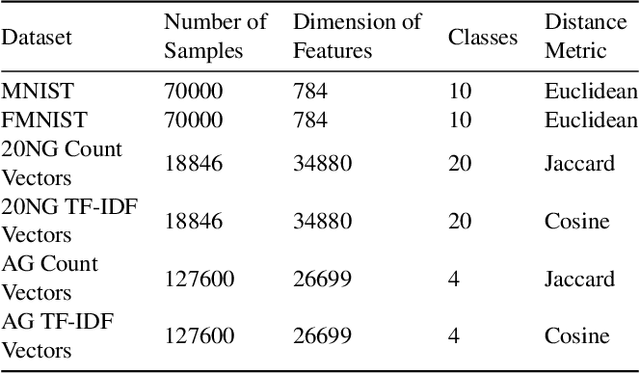
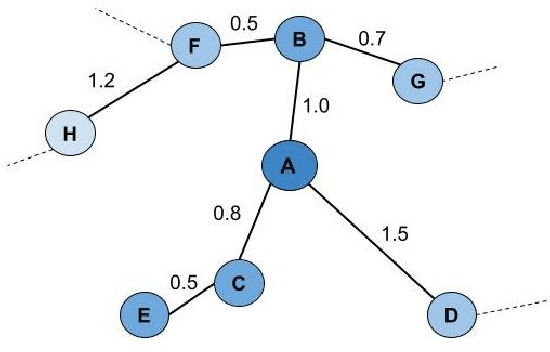
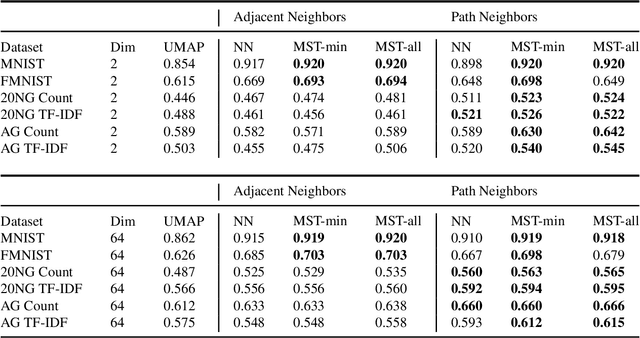
Topology based dimensionality reduction methods such as t-SNE and UMAP have seen increasing success and popularity in high-dimensional data. These methods have strong mathematical foundations and are based on the intuition that the topology in low dimensions should be close to that of high dimensions. Given that the initial topological structure is a precursor to the success of the algorithm, this naturally raises the question: What makes a "good" topological structure for dimensionality reduction? %Insight into this will enable us to design better algorithms which take into account both local and global structure. In this paper which focuses on UMAP, we study the effects of node connectivity (k-Nearest Neighbors vs \textit{mutual} k-Nearest Neighbors) and relative neighborhood (Adjacent via Path Neighbors) on dimensionality reduction. We explore these concepts through extensive ablation studies on 4 standard image and text datasets; MNIST, FMNIST, 20NG, AG, reducing to 2 and 64 dimensions. Our findings indicate that a more refined notion of connectivity (\textit{mutual} k-Nearest Neighbors with minimum spanning tree) together with a flexible method of constructing the local neighborhood (Path Neighbors), can achieve a much better representation than default UMAP, as measured by downstream clustering performance.