Classification with the matrix-variate-$t$ distribution
Paper and Code
Jul 22, 2019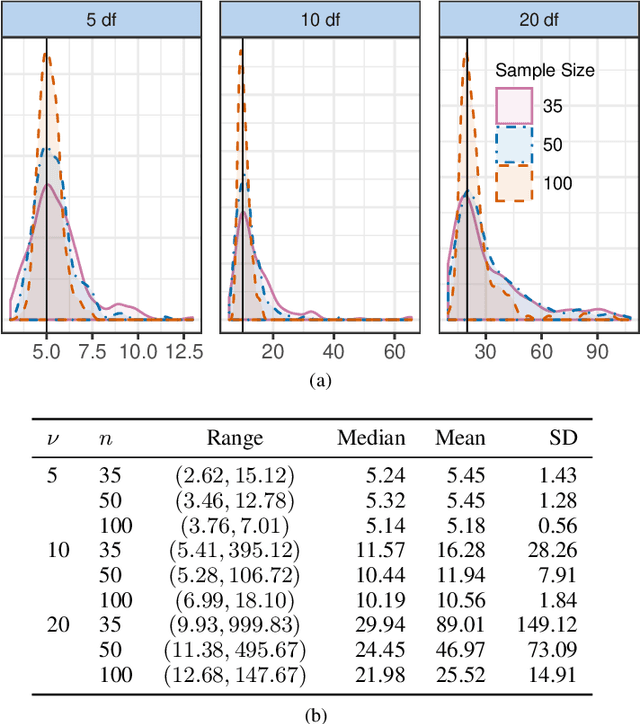
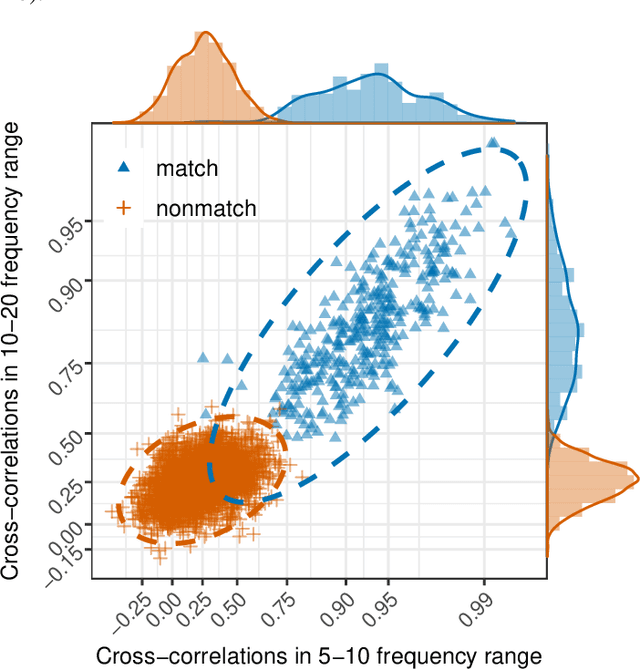
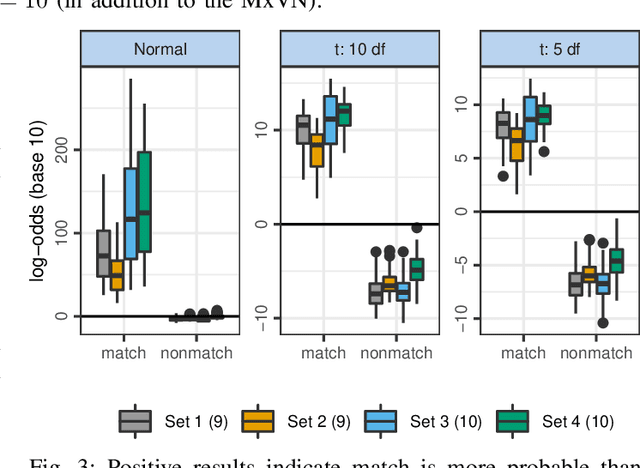
Matrix-variate distributions can intuitively model the dependence structure of matrix-valued observations that arise in applications with multivariate time series, spatio-temporal or repeated measures. This paper develops an Expectation-Maximization algorithm for discriminant analysis and classification with matrix-variate $t$-distributions. The methodology shows promise on simulated datasets or when applied to the forensic matching of fractured surfaces or the classification of functional Magnetic Resonance, satellite or hand gestures images.
* 10 pages, 3 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge