Classification Performance Metric Elicitation and its Applications
Paper and Code
Aug 19, 2022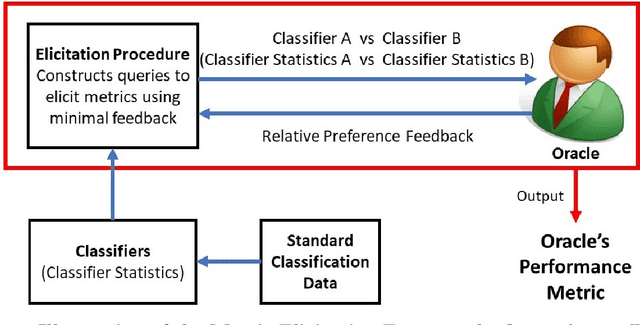



Given a learning problem with real-world tradeoffs, which cost function should the model be trained to optimize? This is the metric selection problem in machine learning. Despite its practical interest, there is limited formal guidance on how to select metrics for machine learning applications. This thesis outlines metric elicitation as a principled framework for selecting the performance metric that best reflects implicit user preferences. Once specified, the evaluation metric can be used to compare and train models. In this manuscript, we formalize the problem of Metric Elicitation and devise novel strategies for eliciting classification performance metrics using pairwise preference feedback over classifiers. Specifically, we provide novel strategies for eliciting linear and linear-fractional metrics for binary and multiclass classification problems, which are then extended to a framework that elicits group-fair performance metrics in the presence of multiple sensitive groups. All the elicitation strategies that we discuss are robust to both finite sample and feedback noise, thus are useful in practice for real-world applications. Using the tools and the geometric characterizations of the feasible confusion statistics sets from the binary, multiclass, and multiclass-multigroup classification setups, we further provide strategies to elicit from a wider range of complex, modern multiclass metrics defined by quadratic functions of confusion statistics by exploiting their local linear structure. From application perspective, we also propose to use the metric elicitation framework in optimizing complex black box metrics that is amenable to deep network training. Lastly, to bring theory closer to practice, we conduct a preliminary real-user study that shows the efficacy of the metric elicitation framework in recovering the users' preferred performance metric in a binary classification setup.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge