Classification of Periodic Variable Stars with Novel Cyclic-Permutation Invariant Neural Networks

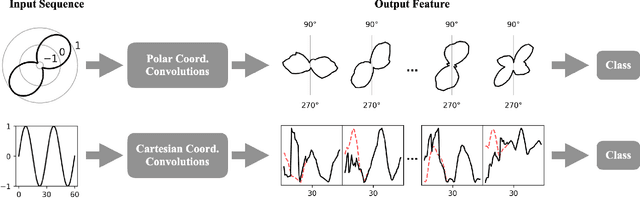
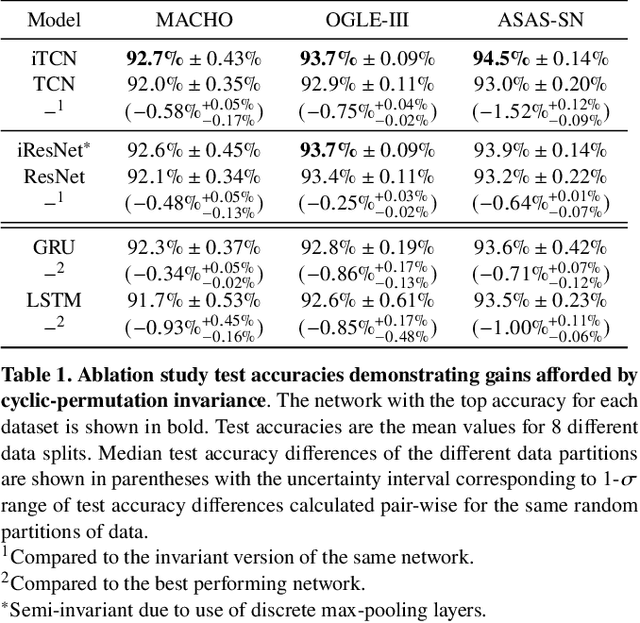
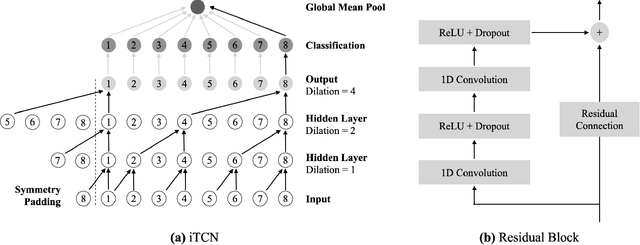
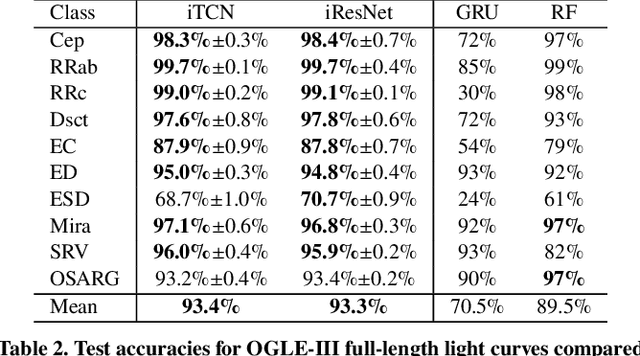
Neural networks (NNs) have been shown to be competitive against state-of-the-art feature engineering and random forest (RF) classification of periodic variable stars. Although previous work utilising NNs has made use of periodicity by period folding multiple-cycle time-series into a single cycle---from time-space to phase-space---no approach to date has taken advantage of the fact that network predictions should be invariant to the initial phase of the period-folded sequence. Initial phase is exogenous to the physical origin of the variability and should thus be factored out. Here, we present cyclic-permutation invariant networks, a novel class of NNs for which invariance to phase shifts is guaranteed through polar coordinate convolutions, which we implement by means of "Symmetry Padding." Across three different datasets of variable star light curves, we show that two implementations of the cyclic-permutation invariant network: the iTCN and the iResNet, consistently outperform non-invariant baselines and reduce overall error rates by between 4% to 22%. Over a 10-class OGLE-III sample, the iTCN/iResNet achieves an average per-class accuracy of 93.4%/93.3%, compared to RNN/RF accuracies of 70.5%/89.5% in a recent study using the same data. Finding improvement on a non-astronomy benchmark, we suggest that the methodology introduced here should also be applicable to a wide range of science domains where periodic data abounds due to physical symmetries.