Checking Trustworthiness of Probabilistic Computations in a Typed Natural Deduction System

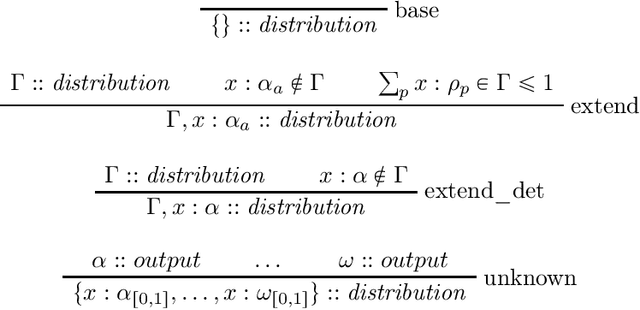
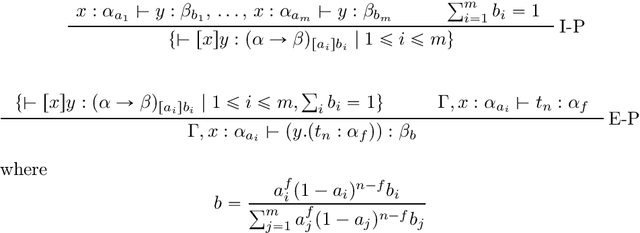
In this paper we present the probabilistic typed natural deduction calculus TPTND, designed to reason about and derive trustworthiness properties of probabilistic computational processes, like those underlying current AI applications. Derivability in TPTND is interpreted as the process of extracting $n$ samples of outputs with a certain frequency from a given categorical distribution. We formalize trust within our framework as a form of hypothesis testing on the distance between such frequency and the intended probability. The main advantage of the calculus is to render such notion of trustworthiness checkable. We present the proof-theoretic semantics of TPTND and illustrate structural and metatheoretical properties, with particular focus on safety. We motivate its use in the verification of algorithms for automatic classification.