Characterizing Well-behaved vs. Pathological Deep Neural Network Architectures
Paper and Code
Nov 07, 2018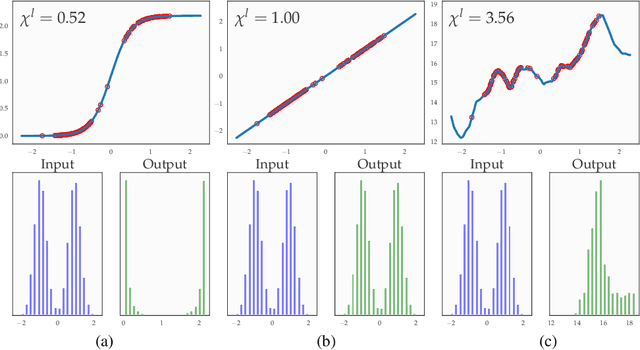
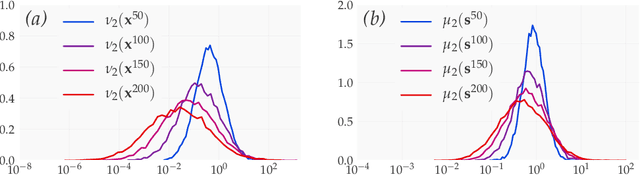
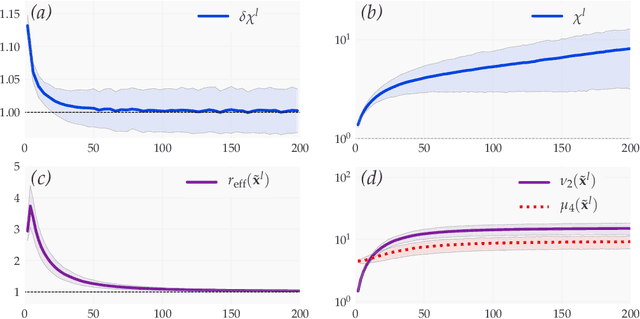
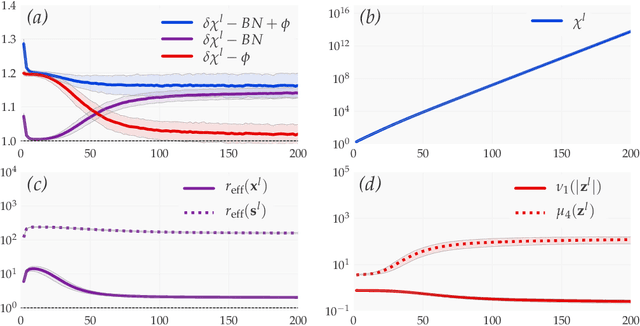
We introduce a principled approach, requiring only mild assumptions, for the characterization of deep neural networks at initialization. Our approach applies both to fully-connected and convolutional networks and incorporates the commonly used techniques of batch normalization and skip-connections. Our key insight is to consider the evolution with depth of statistical moments of signal and sensitivity, thereby characterizing the well-behaved or pathological behaviour of input-output mappings encoded by different choices of architecture. We establish: (i) for feedforward networks with and without batch normalization, depth multiplicativity inevitably leads to ill-behaved moments and distributional pathologies; (ii) for residual networks, on the other hand, the mechanism of identity skip-connection induces power-law rather than exponential behaviour, leading to well-behaved moments and no distributional pathology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge