Chance-Constrained Motion Planning using Modeled Distance-to-Collision Functions
Paper and Code
Jul 22, 2021
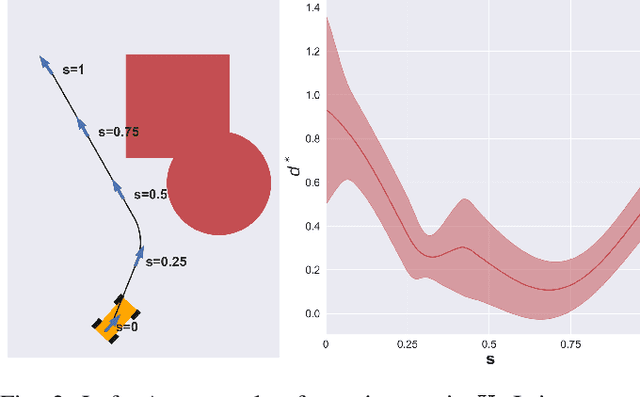
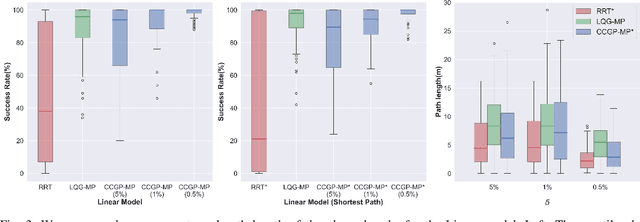
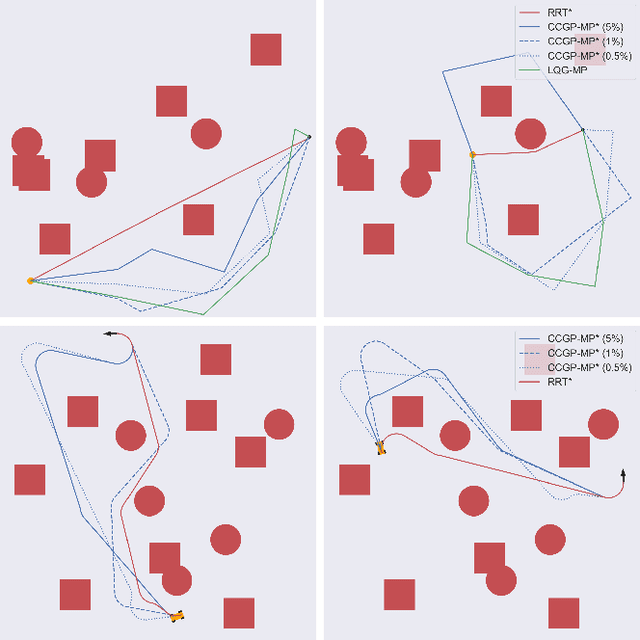
This paper introduces Chance Constrained Gaussian Process-Motion Planning (CCGP-MP), a motion planning algorithm for robotic systems under motion and state estimate uncertainties. The paper's key idea is to capture the variations in the distance-to-collision measurements caused by the uncertainty in state estimation techniques using a Gaussian Process (GP) model. We formulate the planning problem as a chance constraint problem and propose a deterministic constraint that uses the modeled distance function to verify the chance-constraints. We apply Simplicial Homology Global Optimization (SHGO) approach to find the global minimum of the deterministic constraint function along the trajectory and use the minimum value to verify the chance-constraints. Under this formulation, we can show that the optimization function is smooth under certain conditions and that SHGO converges to the global minimum. Therefore, CCGP-MP will always guarantee that all points on a planned trajectory satisfy the given chance-constraints. The experiments in this paper show that CCGP-MP can generate paths that reduce collisions and meet optimality criteria under motion and state uncertainties. The implementation of our robot models and path planning algorithm can be found on GitHub.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge