Certain and Uncertain Inference with Trivalent Conditionals
Paper and Code
Jul 17, 2022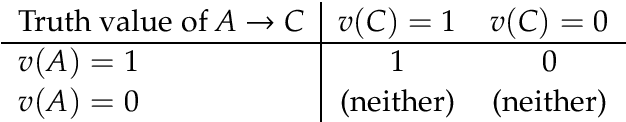
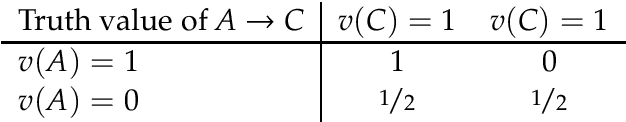
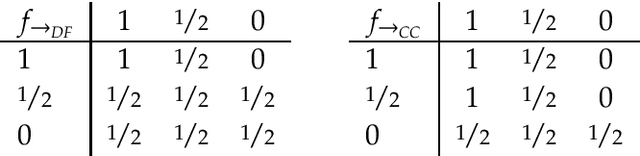
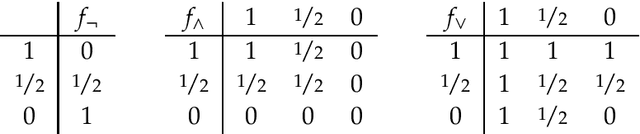
Research on indicative conditionals usually aims either at determining their truth conditions, or at explaining how we should reason with them and when we can assert them. This paper integrates these semantic and epistemological projects by means of articulating trivalent, truth-functional truth conditions for indicative conditionals. Based on this framework, we provide a non-classical account of the probability of conditionals, and two logics of conditional reasoning: (i) a logic C of inference from certain premises that generalizes deductive reasoning; and (ii) a logic U of inference from uncertain premises that generalizes defeasible reasoning. Both logics are highly attractive in their domain. They provide a unified framework for conditional reasoning, generalize existing theories (e.g., Adams's logic of "reasonable inference") and yield an insightful analysis of the controversies about the validity of Modus Ponens, Import-Export, and other principles of conditional logic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge