Causality-aware counterfactual confounding adjustment as an alternative to linear residualization in anticausal prediction tasks based on linear learners
Paper and Code
Nov 09, 2020

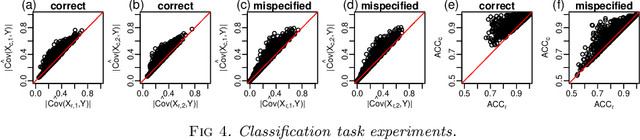
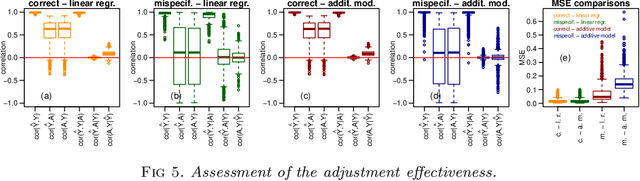
Linear residualization is a common practice for confounding adjustment in machine learning (ML) applications. Recently, causality-aware predictive modeling has been proposed as an alternative causality-inspired approach for adjusting for confounders. The basic idea is to simulate counterfactual data that is free from the spurious associations generated by the observed confounders. In this paper, we compare the linear residualization approach against the causality-aware confounding adjustment in anticausal prediction tasks, and show that the causality-aware approach tends to (asymptotically) outperform the residualization adjustment in terms of predictive performance in linear learners. Importantly, our results still holds even when the true model is not linear. We illustrate our results in both regression and classification tasks, where we compared the causality-aware and residualization approaches using mean squared errors and classification accuracy in synthetic data experiments where the linear regression model is mispecified, as well as, when the linear model is correctly specified. Furthermore, we illustrate how the causality-aware approach is more stable than residualization with respect to dataset shifts in the joint distribution of the confounders and outcome variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge