Causal Inference Using Linear Time-Varying Filters with Additive Noise

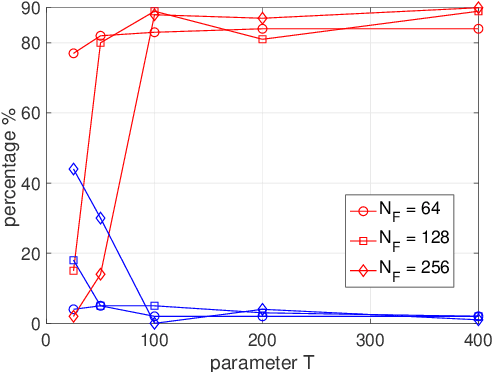
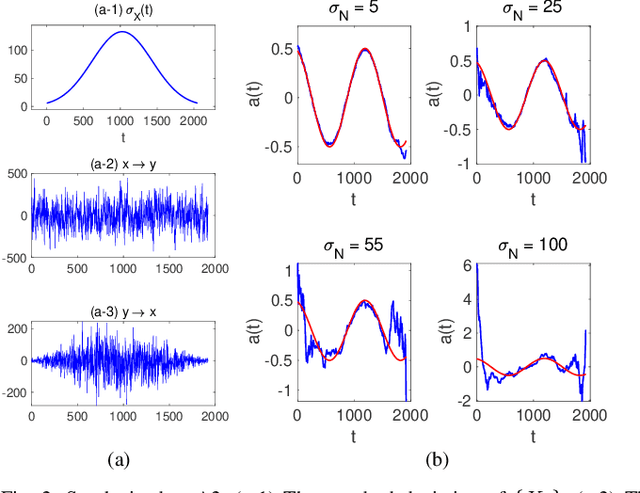
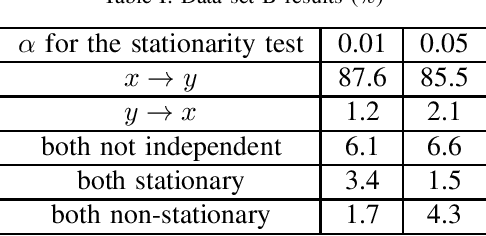
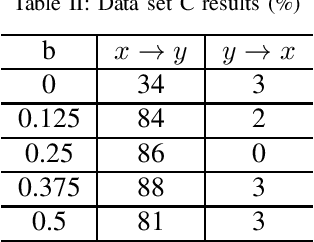
Causal inference using the restricted structural causal model framework hinges largely on the asymmetry between cause and effect from the data generating mechanisms. For linear models and additive noise models, the asymmetry arises from non-Gaussianity or non-linearity, respectively. This methodology can be adapted to stationary time series, however, inferring causal relationships from non-stationary time series remains a challenging task. In the work, we focus on slowly-varying nonstationary processes and propose to break the symmetry by exploiting the nonstationarity of the data. Our main theoretical result shows that causal direction is identifiable in generic cases when cause and effect are connected via a time-varying filter. We propose a causal discovery procedure by leveraging powerful estimates of the bivariate evolutionary spectra. Both synthetic and real-world data simulations that involve high-order and nonsmooth filters are provided to demonstrate the effectiveness of our proposed methodology.