Catch Me if You Can: Effective Honeypot Placement in Dynamic AD Attack Graphs
Paper and Code
Dec 28, 2023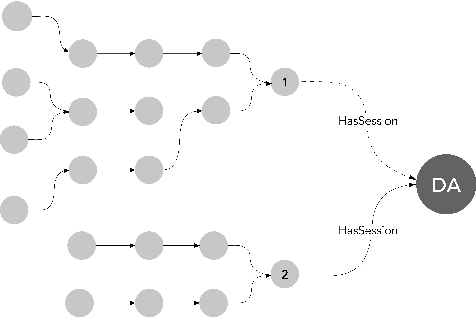
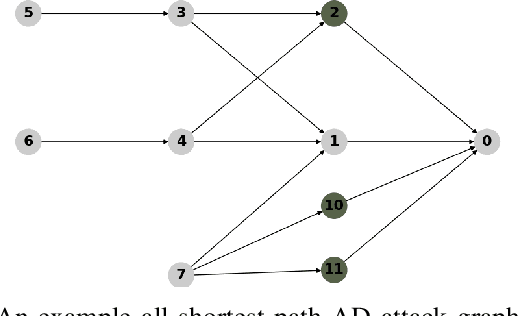
We study a Stackelberg game between an attacker and a defender on large Active Directory (AD) attack graphs where the defender employs a set of honeypots to stop the attacker from reaching high-value targets. Contrary to existing works that focus on small and static attack graphs, AD graphs typically contain hundreds of thousands of nodes and edges and constantly change over time. We consider two types of attackers: a simple attacker who cannot observe honeypots and a competent attacker who can. To jointly solve the game, we propose a mixed-integer programming (MIP) formulation. We observed that the optimal blocking plan for static graphs performs poorly in dynamic graphs. To solve the dynamic graph problem, we re-design the mixed-integer programming formulation by combining m MIP (dyMIP(m)) instances to produce a near-optimal blocking plan. Furthermore, to handle a large number of dynamic graph instances, we use a clustering algorithm to efficiently find the m-most representative graph instances for a constant m (dyMIP(m)). We prove a lower bound on the optimal blocking strategy for dynamic graphs and show that our dyMIP(m) algorithms produce close to optimal results for a range of AD graphs under realistic conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge