Can Electromagnetic Information Theory Improve Wireless Systems? A Channel Estimation Example

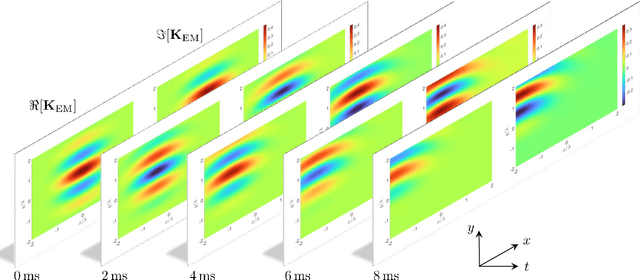
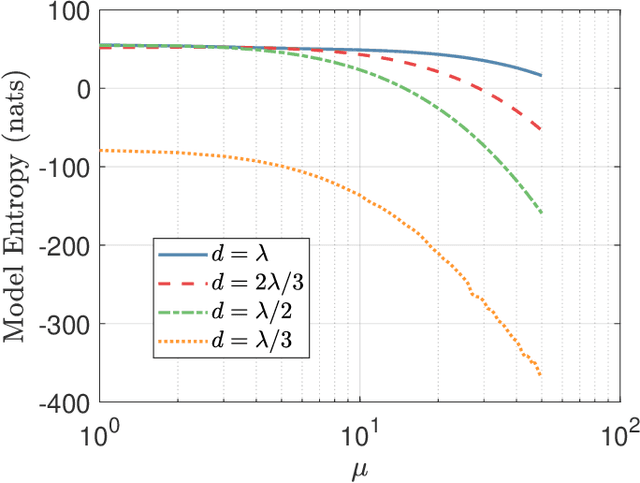
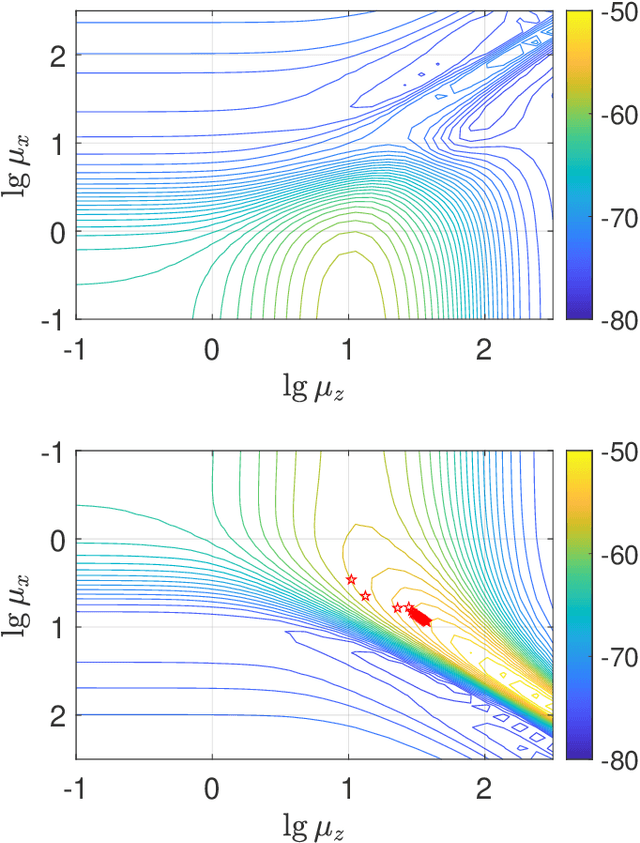
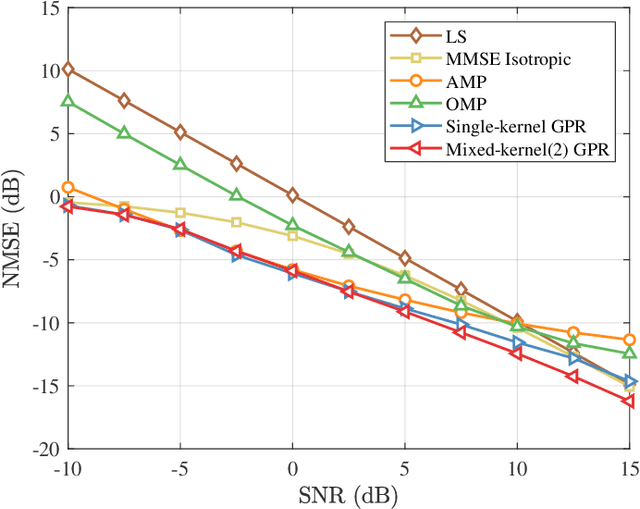
Electromagnetic information theory (EIT) is an emerging interdisciplinary subject that integrates classical Maxwell electromagnetics and Shannon information theory. The goal of EIT is to uncover the information transmission mechanisms from an electromagnetic (EM) perspective in wireless systems. Existing works on EIT are mainly focused on the analysis of degrees-of-freedom (DoF), system capacity, and characteristics of the electromagnetic channel. However, these works do not clarify how EIT can improve wireless communication systems. To answer this question, in this paper, we provide a novel demonstration of the application of EIT. By integrating EM knowledge into the classical MMSE channel estimator, we observe for the first time that EIT is capable of improving the channel estimation performace. Specifically, the EM knowledge is first encoded into a spatio-temporal correlation function (STCF), which we term as the EM kernel. This EM kernel plays the role of side information to the channel estimator. Since the EM kernel takes the form of Gaussian processes (GP), we propose the EIT-based Gaussian process regression (EIT-GPR) to derive the channel estimations. In addition, since the EM kernel allows parameter tuning, we propose EM kernel learning to fit the EM kernel to channel observations. Simulation results show that the application of EIT to the channel estimator enables it to outperform traditional isotropic MMSE algorithm, thus proving the practical values of EIT.