Can a single neuron learn quantiles?
Paper and Code
Jun 07, 2021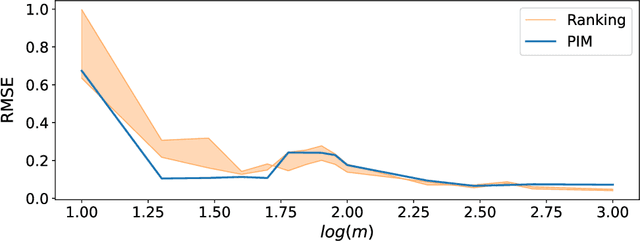

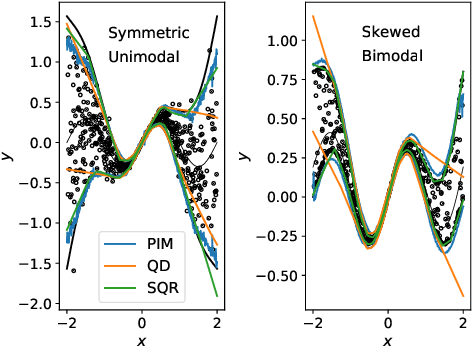
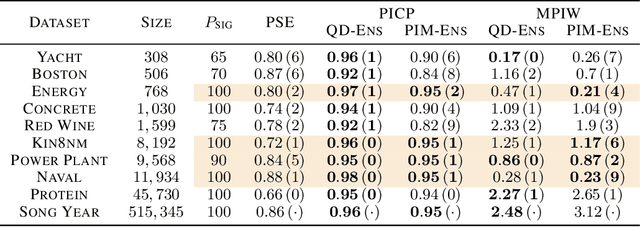
A novel non-parametric quantile estimation method for continuous random variables is introduced, based on a minimal neural network architecture consisting of a single unit. Its advantage over estimations from ranking the order statistics is shown, specifically for small sample size. In a regression context, the method can be used to quantify predictive uncertainty under the split conformal prediction setting, where prediction intervals are estimated from the residuals of a pre-trained model on a held-out validation set to quantify the uncertainty in future predictions. Benchmarking experiments demonstrate that the method is competitive in quality and coverage with state-of-the-art solutions, with the added benefit of being more computationally efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge