Calibration with Bias-Corrected Temperature Scaling Improves Domain Adaptation Under Label Shift in Modern Neural Networks

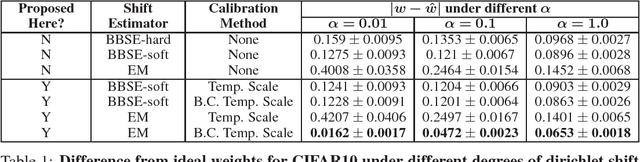
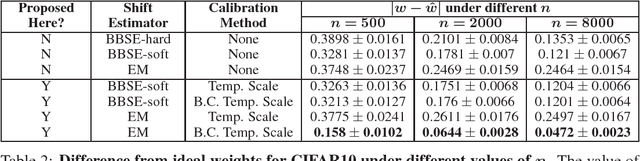
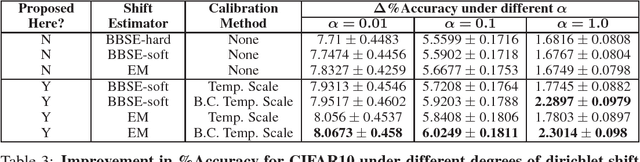
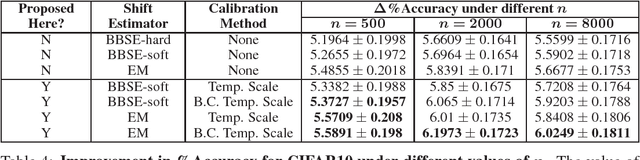
Label shift refers to the phenomenon where the marginal probability p(y) of observing a particular class changes between the training and test distributions while the conditional probability p(x|y) stays fixed. This is relevant in settings such as medical diagnosis, where a classifier trained to predict disease based on observed symptoms may need to be adapted to a different distribution where the baseline frequency of the disease is higher. Given calibrated estimates of p(y|x), one can apply an EM algorithm to correct for the shift in class imbalance between the training and test distributions without ever needing to calculate p(x|y). Unfortunately, modern neural networks typically fail to produce well-calibrated probabilities, compromising the effectiveness of this approach. Although Temperature Scaling can greatly reduce miscalibration in these networks, it can leave behind a systematic bias in the probabilities that still poses a problem. To address this, we extend Temperature Scaling with class-specific bias parameters, which largely eliminates systematic bias in the calibrated probabilities and allows for effective domain adaptation under label shift. We term our calibration approach "Bias-Corrected Temperature Scaling". On experiments with CIFAR10, we find that EM with Bias-Corrected Temperature Scaling significantly outperforms both EM with Temperature Scaling and the recently-proposed Black-Box Shift Estimation.