Calculation of Sub-bands {1,2,5,6} for 64-Point Complex FFT and Its extension to N Point FFT

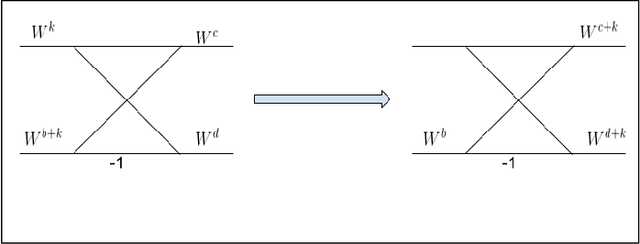
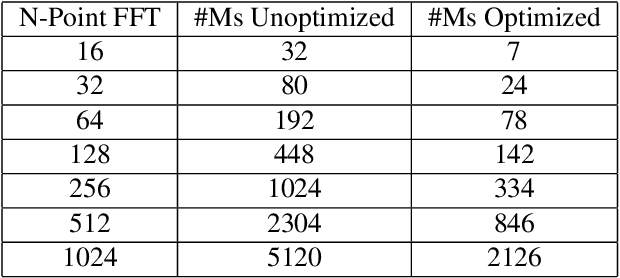
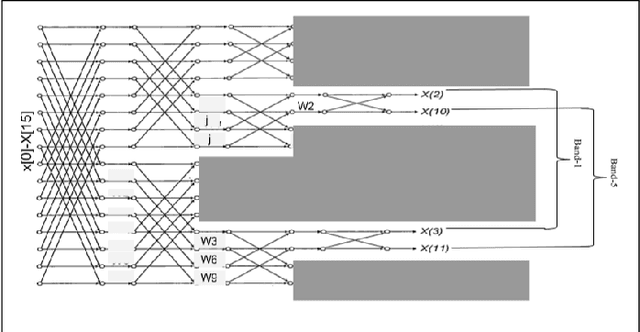
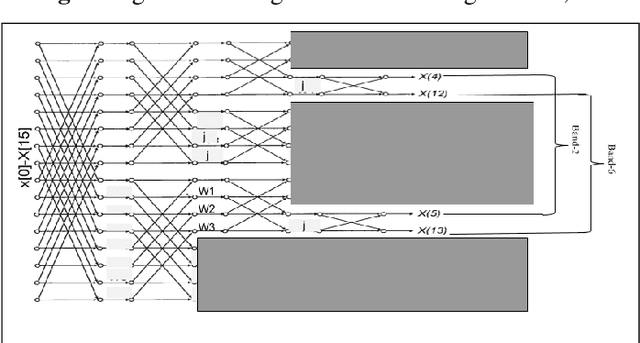
FFT algorithm is one of the most applied algorithmsin digital signal processing. Digital signal processing hasgradually become important in biomedical application. Herehardware implementation of FFTs have found useful appli-cations for bio-wearable devices. However, for these devices, low-power and low-area are of utmost importance.In this report, we investigate a sub-structure of decimation-in-frequency (DIF) FFT where a number of sub-bands areof interest to us. Specifically, we divide the range of frequencies into 8 sub-bands (0-7) and calculate 4 of them( 1,2,5,6). We show that using concepts likepushingandradix22, the number of complex multiplications can be dras-tically reduced for 16-point, 32-point and 64-point FFTswhile computing those specific bands. Later, we also extendit toN= 2n-point FFT based on optimized 64-point FFTstructure. The number of complex multiplications is furtherreduced usingmerge-FFT. Our results show that the numberof multiplications (and hence power) can be reduced greatlyusing our optimized structure compared to an unoptimizedstructure. This can find application in biomedical signal processing specifically while computingp ower spectral density of a physiological time series where reducing computational power is of utmost importance