Calabi-Yau Metrics, Energy Functionals and Machine-Learning
Paper and Code
Dec 20, 2021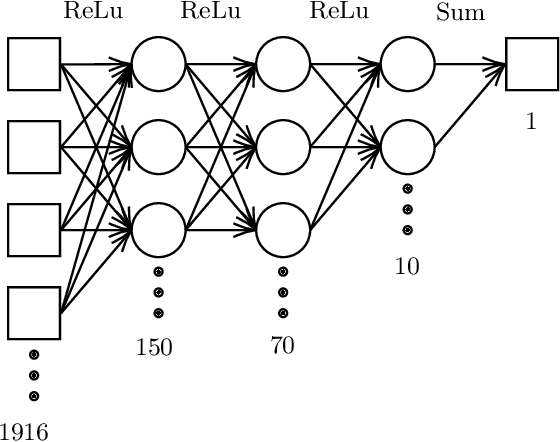
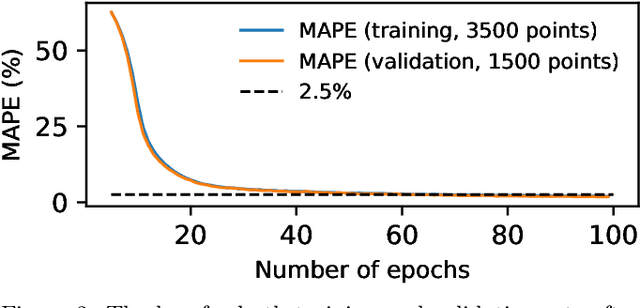
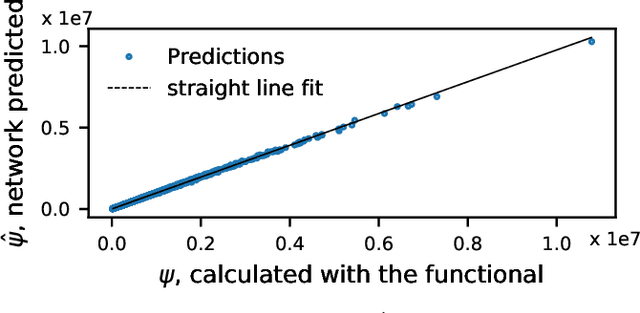
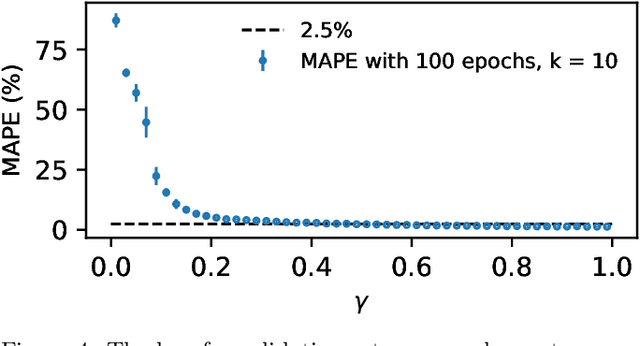
We apply machine learning to the problem of finding numerical Calabi-Yau metrics. We extend previous work on learning approximate Ricci-flat metrics calculated using Donaldson's algorithm to the much more accurate "optimal" metrics of Headrick and Nassar. We show that machine learning is able to predict the K\"ahler potential of a Calabi-Yau metric having seen only a small sample of training data.
* 7 pages, 5 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge