Budget-Constrained Reinforcement of Ranked Objects
Paper and Code
Mar 27, 2022

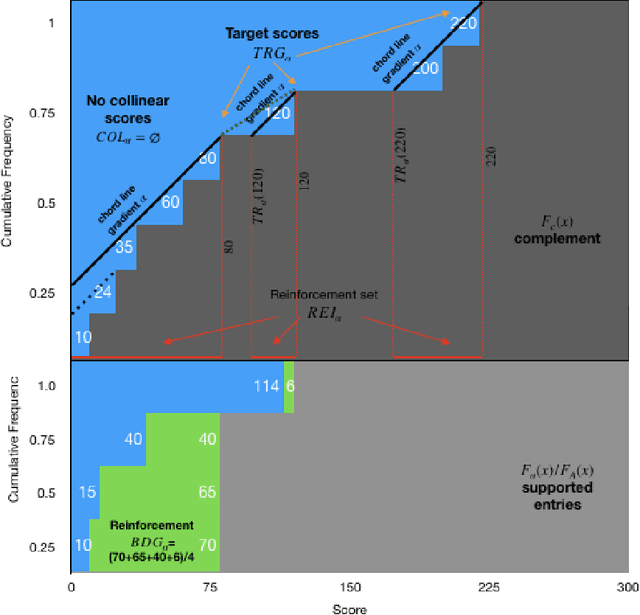
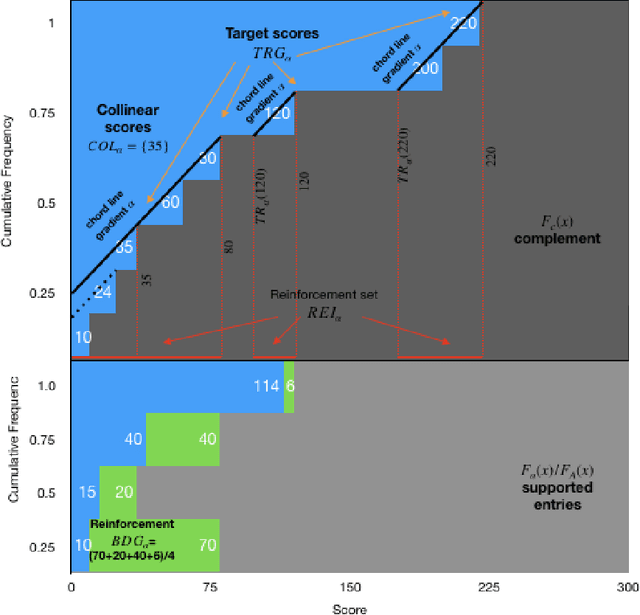
Commercial entries, such as hotels, are ranked according to score by a search engine or recommendation system, and the score of each can be improved upon by making a targeted investment, e.g., advertising. We study the problem of how a principal, who owns or supports a set of entries, can optimally allocate a budget to maximize their ranking. Representing the set of ranked scores as a probability distribution over scores, we treat this question as a game between distributions. We show that, in the general case, the best ranking is achieved by equalizing the scores of several disjoint score ranges. We show that there is a unique optimal reinforcement strategy, and provide an efficient algorithm implementing it.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge